题目内容
已知一元二次方程ax2+bx+c=0的两根之和为p,两根平方和为q,两根立方和为r,则ar+bq+cp的值是
- A.-1
- B.0
- C.1
- D.2
B
分析:根据根与系数的关系,设方程ax2+bx+c=0的两个实根为x1,x2,利用根与系数的关系及完全平方公式用x1,x2表达出p,q及r,代入所求式子中化简即可求出值.
解答:设方程ax2+bx+c=0的两个实根为x1,x2,
则为x1+x2=- ,x1x2=
,x1x2= ,
,
又p=x1+x2=- ,q=x12+x22=(x1+x2)2-2x1x2=
,q=x12+x22=(x1+x2)2-2x1x2= -
-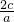 ,
,
r=x13+x23=(x1+x2)(x12+x12-x1x2)= (
(  -
-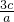 ),
),
∴ar+bq+cp
=-b( -
-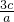 )+b(
)+b(  -
-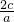 )+c(-
)+c(- )
)
=-b• +b•
+b• -
-
=- +
+ +
+ -
- -
-
= -
- -
-
=0.
故选B
点评:本题考查了根与系数的关系,完全平方公式的运用,以及分式的混合运算,难度适中,设出方程两解后,把两根之和为p,两根平方和为q,两根立方和为r化为关于x1+x2,及x1x2的关系式是解本题的关键,此外在运算过程中要细心认真,不要出错.
分析:根据根与系数的关系,设方程ax2+bx+c=0的两个实根为x1,x2,利用根与系数的关系及完全平方公式用x1,x2表达出p,q及r,代入所求式子中化简即可求出值.
解答:设方程ax2+bx+c=0的两个实根为x1,x2,
则为x1+x2=-
 ,x1x2=
,x1x2= ,
,又p=x1+x2=-
 ,q=x12+x22=(x1+x2)2-2x1x2=
,q=x12+x22=(x1+x2)2-2x1x2= -
-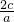 ,
,r=x13+x23=(x1+x2)(x12+x12-x1x2)=
 (
(  -
-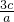 ),
),∴ar+bq+cp
=-b(
 -
-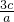 )+b(
)+b(  -
-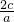 )+c(-
)+c(- )
)=-b•
 +b•
+b• -
-
=-
 +
+ +
+ -
- -
-
=
 -
- -
-
=0.
故选B
点评:本题考查了根与系数的关系,完全平方公式的运用,以及分式的混合运算,难度适中,设出方程两解后,把两根之和为p,两根平方和为q,两根立方和为r化为关于x1+x2,及x1x2的关系式是解本题的关键,此外在运算过程中要细心认真,不要出错.

练习册系列答案
相关题目
 时,求出此二次函数的解析式;
时,求出此二次函数的解析式; ,若存在求出P点坐标,若不存在请说明理由.
,若存在求出P点坐标,若不存在请说明理由. 时,求出此二次函数的解析式;
时,求出此二次函数的解析式; ,若存在求出P点坐标,若不存在请说明理由.
,若存在求出P点坐标,若不存在请说明理由.