题目内容
已知关于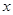 的方程
的方程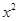 -(k+2)
-(k+2)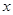 +2k=0
+2k=0
(1)说明:无论k取何值,方程总有实数根;
(2)若方程有两个相等的实数根,求出方程的根.
【答案】
(1)详见解析;(2)2
【解析】
试题分析:一元二次方程根的情况与判别式△ 的关系:(1)
的关系:(1) 方程有两个不相等的实数根;(2)
方程有两个不相等的实数根;(2) 方程有两个相等的实数根;(3)
方程有两个相等的实数根;(3) 方程没有实数根.
方程没有实数根.
(1)由△ 即可作出判断;
即可作出判断;
(2)由方程有两个相等的实数根可得△ ,即得
,即得 ,即可求得k的值,从而可以求得方程的根.
,即可求得k的值,从而可以求得方程的根.
试题解析:(1)∵△
∴无论k取何值,方程总有实数根;
(2)由题意得△
 ,解得
,解得
则原方程可化为 ,解得
,解得
 .
.
考点:1.一元二次方程根的情况与判别式;2.解一元二次方程

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知关于的方程
=-1有正根,则实数a的取值范围是( )
| x+a |
| x-3 |
| A、a<0且a≠-3 |
| B、a>0 |
| C、a<-3 |
| D、a<3且a≠-3 |
 的方程
的方程 .
.
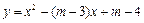 与
与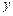 轴交于点M,若抛物线与x轴的一个交点关于直线
轴交于点M,若抛物线与x轴的一个交点关于直线 的对称点恰好是点M,求
的对称点恰好是点M,求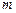 的值.
的值.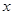 的方程
的方程
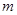 的值,并求出此时方程的根(6分)
的值,并求出此时方程的根(6分)