题目内容
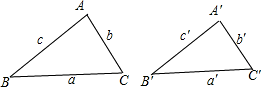 如图,△ABC与△A′B′C′的三边分别为a、b、c与a′、b′、c′,且∠B=∠B′,∠A+∠A′=180°.试证:aa′=bb′+cc′.
如图,△ABC与△A′B′C′的三边分别为a、b、c与a′、b′、c′,且∠B=∠B′,∠A+∠A′=180°.试证:aa′=bb′+cc′.
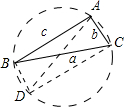 证明:作△ABC的外接圆,过C作CD∥AB交圆于D,连接AD和BD,如图所示.
证明:作△ABC的外接圆,过C作CD∥AB交圆于D,连接AD和BD,如图所示.∵∠A+∠A'=180°=∠A+∠D,
∠BCD=∠B=∠B',
∴∠A'=∠D,∠B'=∠BCD.
∴△A'B'C'∽△DCB.
有
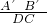 =
=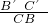 =
=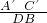 ,
,即
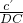 =
=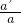 =
= .
.故DC=
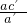 ,DB=
,DB=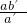 .
.又AB∥DC,可知BD=AC=b,BC=AD=a.
从而,由托勒密定理,得
AD•BC=AB•DC+AC•BD,
即a2=c•
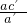 +b•
+b•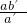 .
.故aa'=bb'+cc'.
分析:因∠B=∠B',∠A+∠A'=180°,由结论联想到构造圆内接四边形加以证明,故作△ABC的外接圆,过C作CD∥AB交圆于D,连接AD和BD,即可求证△A'B'C'∽△DCB,由托勒密定理,得AD•BC=AB•DC+AC•BD,即可解题.
点评:本题考查了相似三角形的证明和相似三角形对应边比值相等的性质,考查了托勒密定理的应用,本题中求证△A'B'C'∽△DCB是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
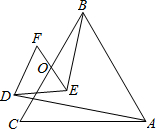 如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为( )
如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为( )A、
| ||
B、
| ||
| C、5:3 | ||
| D、不确定 |
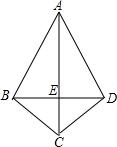 如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为
如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为 22、如图,△ABC与△ADE是两个大小不同的等腰直角三角形,B、C、E在同一条直线上,连接CD.
22、如图,△ABC与△ADE是两个大小不同的等腰直角三角形,B、C、E在同一条直线上,连接CD.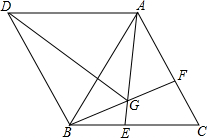 如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.
如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G. 29、如图,△ABC与△A′B′C′关于直线MN对称,△A′B′C′与△A″B″C″关于直线EF对称.
29、如图,△ABC与△A′B′C′关于直线MN对称,△A′B′C′与△A″B″C″关于直线EF对称.