题目内容
 (2012•东城区二模)如图,在平行四边形ABCD中,AB=5,BC=8,AE⊥BC于点E,cosB=
(2012•东城区二模)如图,在平行四边形ABCD中,AB=5,BC=8,AE⊥BC于点E,cosB=| 3 | 5 |
分析:首先由已知条件和勾股定理计算CE=5,所以CD=AB,进而得到∠CDE=∠CED=∠ADE,所以tan∠CDE=tan∠ADE问题的解.
解答:解:在△ABE中,AE⊥BC,AB=5,cosB=
,
∴BE=3,AE=4.
∴EC=BC-BE=8-3=5.
∵平行四边形ABCD,
∴CD=AB=5.
∴△CED为等腰三角形.
∴∠CDE=∠CED.
∵AD∥BC,
∴∠ADE=∠CED.
∴∠CDE=∠ADE.
在Rt△ADE中,AE=4,AD=BC=8,
∴tan∠CDE=
=
.
| 3 |
| 5 |
∴BE=3,AE=4.
∴EC=BC-BE=8-3=5.
∵平行四边形ABCD,

∴CD=AB=5.
∴△CED为等腰三角形.
∴∠CDE=∠CED.
∵AD∥BC,
∴∠ADE=∠CED.
∴∠CDE=∠ADE.
在Rt△ADE中,AE=4,AD=BC=8,
∴tan∠CDE=
| 4 |
| 8 |
| 1 |
| 2 |
点评:本题考查了解直角三角形的运用、勾股定理的运用、平行四边形的性质和等腰三角形的判定和性质,解题的关键是找到图形中相等的角.

练习册系列答案
相关题目
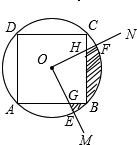 (2012•东城区二模)如图,正方形ABCD内接于⊙O,⊙O的半径为2,以圆心O为顶点作∠MON,使∠MON=90°,OM、ON分别与⊙O交于点E、F,与正方形ABCD的边交于点G、H,则由OE、OF、
(2012•东城区二模)如图,正方形ABCD内接于⊙O,⊙O的半径为2,以圆心O为顶点作∠MON,使∠MON=90°,OM、ON分别与⊙O交于点E、F,与正方形ABCD的边交于点G、H,则由OE、OF、
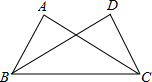 (2012•东城区二模)已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.
(2012•东城区二模)已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.