题目内容
 如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-
如图所示,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=- +b交折线OAB于点E.记△ODE的面积为S,求S与b的函数关系式.
+b交折线OAB于点E.记△ODE的面积为S,求S与b的函数关系式.
解:(1)由题意得B(3,1).
若直线经过点A(3,0)时,则b= ;
;
若直线经过点B(3,1)时,则b= ;
;
若直线经过点C(0,1)时,则b=1;
①若直线与折线OAB的交点在OA上时,即1<b≤ ,如图①,
,如图①,
此时E(2b,0)
∴S= OE•CO=
OE•CO= ×2b×1=b
×2b×1=b
②若直线与折线OAB的交点在BA上时,即 <b<
<b< ,如图②
,如图②
此时E(3, ),D(2b-2,1)
),D(2b-2,1)
∴S=S矩-(S△OCD+S△OAE+S△DBE)
=3-[ (2b-2)×1+
(2b-2)×1+ ×(5-2b)•(
×(5-2b)•( )+
)+ ×3(
×3( )]=
)]=
∴S= .
.
分析:分类讨论:直线y=- +b经过C点,A点或B点,得到b的范围为:1≤b≤
+b经过C点,A点或B点,得到b的范围为:1≤b≤ ,或
,或 <b<
<b< ,根据E点坐标表示出有关线段,然后分别根据三角形的面积公式进行计算即可.
,根据E点坐标表示出有关线段,然后分别根据三角形的面积公式进行计算即可.
点评:本题考查了一次函数的性质:点在函数图象上,点的坐标满足函数的解析式.也考查了分类讨论思想的运用和用坐标表示线段的长以及三角形的面积公式.
若直线经过点A(3,0)时,则b=
 ;
;若直线经过点B(3,1)时,则b=
 ;
;若直线经过点C(0,1)时,则b=1;
①若直线与折线OAB的交点在OA上时,即1<b≤
 ,如图①,
,如图①,此时E(2b,0)
∴S=
 OE•CO=
OE•CO= ×2b×1=b
×2b×1=b②若直线与折线OAB的交点在BA上时,即
 <b<
<b< ,如图②
,如图②此时E(3,
 ),D(2b-2,1)
),D(2b-2,1)∴S=S矩-(S△OCD+S△OAE+S△DBE)
=3-[
 (2b-2)×1+
(2b-2)×1+ ×(5-2b)•(
×(5-2b)•( )+
)+ ×3(
×3( )]=
)]=
∴S=
 .
.
分析:分类讨论:直线y=-
 +b经过C点,A点或B点,得到b的范围为:1≤b≤
+b经过C点,A点或B点,得到b的范围为:1≤b≤ ,或
,或 <b<
<b< ,根据E点坐标表示出有关线段,然后分别根据三角形的面积公式进行计算即可.
,根据E点坐标表示出有关线段,然后分别根据三角形的面积公式进行计算即可.点评:本题考查了一次函数的性质:点在函数图象上,点的坐标满足函数的解析式.也考查了分类讨论思想的运用和用坐标表示线段的长以及三角形的面积公式.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
 如图所示,四边形OABC为正方形,边长为6,点A,C分别在x轴,y轴的正半轴上,点D在OA上,且D的坐标为(2,0),P是OB上的一动点,试求PD+PA和的最小值是( )
如图所示,四边形OABC为正方形,边长为6,点A,C分别在x轴,y轴的正半轴上,点D在OA上,且D的坐标为(2,0),P是OB上的一动点,试求PD+PA和的最小值是( ) 端点B、C不重合),过点D作直线y=-
端点B、C不重合),过点D作直线y=- (2013•吴中区一模)如图所示,四边形OABC是矩形,点A、C的坐标分别为(6,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-
(2013•吴中区一模)如图所示,四边形OABC是矩形,点A、C的坐标分别为(6,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-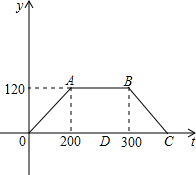 小明参加汽车驾驶培训,在实际操作考试时,被要求进行启动加速、匀速运行、制动减速三个连贯过程,在加速和减速运动过程中,路程和速度均满足关系s=
小明参加汽车驾驶培训,在实际操作考试时,被要求进行启动加速、匀速运行、制动减速三个连贯过程,在加速和减速运动过程中,路程和速度均满足关系s= 如图所示,四边形ABCD与A′B′C′D′以0为位似中心,位似比为1:2.则点A的对应点是点
如图所示,四边形ABCD与A′B′C′D′以0为位似中心,位似比为1:2.则点A的对应点是点