题目内容
(过程探究题)在计算3| 2 |
| 2 |
小芳是这样计算的:3
| 2 |
| 2 |
| 2 |
| 2 |
小红是这样计算的:3
| 2 |
| 2 |
| 2+2 |
| 4 |
小颖是这样计算的:3
| 2 |
| 2 |
| 2 |
| 2 |
你认为谁的解法正确
分析:由于合并同类二次根式的方法只需把同类二次根式的系数相加减,由此即可求解.
解答:解:根据同类项合并即可,
可知小颖的正确.
故答案为:小颖.
可知小颖的正确.
故答案为:小颖.
点评:此题主要考查了合并同类二次根式的方法,和合并同类项的方法实质是一样的.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
如图,在平面直角坐标系中,直角梯形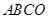 的边
的边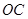 落在
落在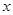 轴的正半轴上,且
轴的正半轴上,且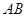 ∥
∥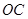 ,
,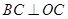 ,
,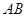 =4,
=4,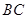 =6,
=6,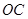 =8.正方形
=8.正方形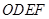 的两边分别落在坐标轴上,且它的面积等于直角梯形
的两边分别落在坐标轴上,且它的面积等于直角梯形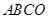 面积。将正方形
面积。将正方形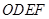 沿
沿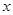 轴的正半轴平行移动,设它与直角梯形
轴的正半轴平行移动,设它与直角梯形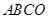 的重叠部分面积为
的重叠部分面积为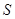 。
。
【小题1】(1)分析与计算:
求正方形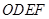 的边长;
的边长;
【小题2】(2)操作与求解:
①正方形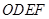 平行移动过程中,通过操作、观察,试判断
平行移动过程中,通过操作、观察,试判断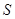 (
(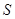 >0)的变化情况是 ;
>0)的变化情况是 ;
②当正方形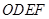 顶点
顶点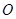 移动到点
移动到点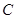 时,求
时,求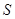 的值;
的值;
【小题3】(3)探究与归纳:
设正方形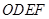 的顶点
的顶点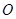 向右移动的距离为
向右移动的距离为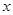 ,求重叠部分面积
,求重叠部分面积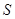 与
与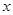 的函数关系式。
的函数关系式。
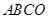 的边
的边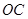 落在
落在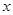 轴的正半轴上,且
轴的正半轴上,且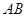 ∥
∥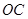 ,
,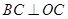 ,
,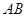 =4,
=4,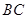 =6,
=6,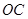 =8.正方形
=8.正方形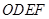 的两边分别落在坐标轴上,且它的面积等于直角梯形
的两边分别落在坐标轴上,且它的面积等于直角梯形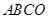 面积。将正方形
面积。将正方形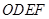 沿
沿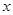 轴的正半轴平行移动,设它与直角梯形
轴的正半轴平行移动,设它与直角梯形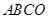 的重叠部分面积为
的重叠部分面积为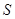 。
。【小题1】(1)分析与计算:
求正方形
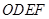 的边长;
的边长;【小题2】(2)操作与求解:
①正方形
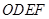 平行移动过程中,通过操作、观察,试判断
平行移动过程中,通过操作、观察,试判断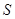 (
(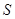 >0)的变化情况是 ;
>0)的变化情况是 ;| A.逐渐增大 | B.逐渐减少 | C.先增大后减少 | D.先减少后增大 |
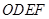 顶点
顶点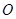 移动到点
移动到点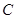 时,求
时,求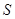 的值;
的值;【小题3】(3)探究与归纳:
设正方形
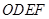 的顶点
的顶点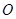 向右移动的距离为
向右移动的距离为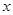 ,求重叠部分面积
,求重叠部分面积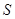 与
与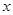 的函数关系式。
的函数关系式。
如图,在平面直角坐标系中,直角梯形 的边
的边 落在
落在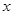 轴的正半轴上,且
轴的正半轴上,且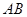 ∥
∥ ,
,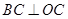 ,
,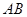 =4,
=4,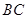 =6,
=6, =8.正方形
=8.正方形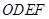 的两边分别落在坐标轴上,且它的面积等于直角梯形
的两边分别落在坐标轴上,且它的面积等于直角梯形 面积。将正方形
面积。将正方形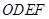 沿
沿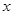 轴的正半轴平行移动,设它与直角梯形
轴的正半轴平行移动,设它与直角梯形 的重叠部分面积为
的重叠部分面积为 。
。
【小题1】(1)分析与计算:
求正方形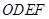 的边长;
的边长;
【小题2】(2)操作与求解:
①正方形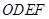 平行移动过程中,通过操作、观察,试判断
平行移动过程中,通过操作、观察,试判断 (
( >0)的变化情况是 ;
>0)的变化情况是 ;
| A.逐渐增大 | B.逐渐减少 | C.先增大后减少 | D.先减少后增大 |
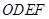 顶点
顶点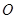 移动到点
移动到点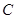 时,求
时,求 的值;
的值;【小题3】(3)探究与归纳:
设正方形
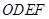 的顶点
的顶点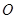 向右移动的距离为
向右移动的距离为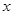 ,求重叠部分面积
,求重叠部分面积 与
与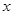 的函数关系式。
的函数关系式。

