题目内容
已知二次三项式ax2+bx+c(a>0)
(1)当c<0时,求函数y=-2|ax2+bx+c|-1的最大值;
(2)若无论k为何实数,直线y=k(x-1)-
与抛物线y=ax2+bx+c有且只有一个公共点,求a+b+c的值.
(1)当c<0时,求函数y=-2|ax2+bx+c|-1的最大值;
(2)若无论k为何实数,直线y=k(x-1)-
| k2 |
| 4 |
(1)由a>0,c<0知y'=ax2+bx+c与x轴必有交点,
y'min<0,
故y=-2|ax2+bx+c|-1的最大值为-1;
(2)联立方程组
,
∴ax2+bx+c=k(x-1)-
k2,
整理得,ax2+(b-k)x+c+k+
k2=0,
∵无论k为何实数,直线与抛物线都只有一个交点,
∴△=(b-k)2-4a(c+k+
k2)=(1-a)k2-2k(2a+b)+b2-4ac=0,
可得1-a=0,2a+b=0,b2-4ac=0,
解得a=1,b=-2,c=1,
故a+b+c=0.
y'min<0,
故y=-2|ax2+bx+c|-1的最大值为-1;
(2)联立方程组
|
∴ax2+bx+c=k(x-1)-
| 1 |
| 4 |
整理得,ax2+(b-k)x+c+k+
| 1 |
| 4 |
∵无论k为何实数,直线与抛物线都只有一个交点,
∴△=(b-k)2-4a(c+k+
| 1 |
| 4 |
可得1-a=0,2a+b=0,b2-4ac=0,
解得a=1,b=-2,c=1,
故a+b+c=0.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
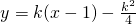 与抛物线y=ax2+bx+c有且只有一个公共点,求a+b+c的值.
与抛物线y=ax2+bx+c有且只有一个公共点,求a+b+c的值. 与抛物线y=ax2+bx+c有且只有一个公共点,求a+b+c的值.
与抛物线y=ax2+bx+c有且只有一个公共点,求a+b+c的值. 与抛物线y=ax2+bx+c有且只有一个公共点,求a+b+c的值.
与抛物线y=ax2+bx+c有且只有一个公共点,求a+b+c的值.