题目内容
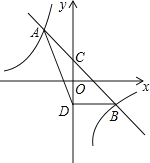
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于A(﹣1,n)、B(2,﹣1)两点,与y轴相交于点C,BD垂直于y轴于点D.
的图象相交于A(﹣1,n)、B(2,﹣1)两点,与y轴相交于点C,BD垂直于y轴于点D.
(1)求一次函数与反比例函数的表达式;
(2)求△ABD的面积;
(3)若M(x,y)、N(x,y)是反比例函数y=![]() 上的两点,当x<x<0时,直接写出y与y的大小关系
上的两点,当x<x<0时,直接写出y与y的大小关系
【答案】(1)y=﹣x+1,y=﹣![]() ;(2)S△ADB=3;(3)y2>y1.
;(2)S△ADB=3;(3)y2>y1.
【解析】
(1)把B点坐标代入y=![]() 得m=﹣2,则反比例函数解析式为y=﹣
得m=﹣2,则反比例函数解析式为y=﹣![]() ,再利用反比例函数解析式确定A点坐标;然后利用待定系数法求出一次函数解析式;
,再利用反比例函数解析式确定A点坐标;然后利用待定系数法求出一次函数解析式;
(2)利用一次函数解析式确定C(﹣4,0),根据三角形面积公式,利用S△AOB=S△AOC+S△BOC进行计算;
(3)根据反比例函数的性质求解.
(1)把B(2,﹣1)代入y=![]() 得m=2×(﹣1)=﹣2;
得m=2×(﹣1)=﹣2;
∴反比例函数解析式为y=﹣![]() ,
,
把A(﹣1,n)代入y=﹣![]() 得﹣n=﹣2,解得n=2;
得﹣n=﹣2,解得n=2;
把A(﹣1,2),B(2,﹣1)分别代入y=kx+b得![]() ,
,
解得![]() ,
,
∴一次函数解析式为y=﹣x+1,
当y=0时,﹣x+1=0,解得x=1,则C(1,0)
∵S△ADB=S△ADC﹣S△BDC=![]() ×2×1+
×2×1+![]() ×2×2=3;
×2×2=3;
(3)y2>y1.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目