题目内容
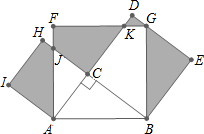如图，直角三角形ABC，∠ACB=90°，分别以AC、BC、AB为边在AB的同侧作正方形，形成了三块阴影部分，记阴影AIHJ的面积为S1，阴影DKGBE的面积为S2，阴影FJCK的面积为S3，若S1=8，S2=9，S3=7，则S△ABC=10
10
．分析：根据题给图形得：AB2+AC2+BC2=S1+S2+S3+2S△ACJ+2S四边形BCKG+S△ABC和AB2=S△ACJ+S四边形BCKG+S△ABC+S3，联立两式即可得出S△ABC．
解答：解：根据题意得：AB2+AC2+BC2=S1+S2+S3+2S△ACJ+2S四边形BCKG+S△ABC ①式，
又AB2=S△ACJ+S四边形BCKG+S△ABC+S3 ②式，
在Rt△ABC中，由勾股定理得：AB2=AC2+BC2，
∴②×2-①得：0=S△ABC+S3-S1-S2，
∴S△ABC=S1+S2-S3=8+9-7=10．
故答案为：10．
又AB2=S△ACJ+S四边形BCKG+S△ABC+S3 ②式，
在Rt△ABC中，由勾股定理得：AB2=AC2+BC2，
∴②×2-①得：0=S△ABC+S3-S1-S2，
∴S△ABC=S1+S2-S3=8+9-7=10．
故答案为：10．
点评：本题考查面积及等积变换的知识，有一定难度，解题关键是将勾股定理和正方形的面积公式进行灵活的结合和应用．
练习册系列答案
阅读快车系列答案
相关题目
如图，直角三角形ABC中∠ACB=90°，CD是高，∠A=30°，AB=4．则BD=
如图，直角三角形ABC的直角边AB=6，以AB为直径画半圆，若阴影部分的面积S1-S2=
如图在直角三角形ABC的斜边AB上另作直角三角形ABD，并以AB为斜边，若BC=1，AC=m，AD=2，则BD等于（ ）
如图，直角三角形ACB中，CD是斜边AB上的中线，若AC=8cm，BC=6cm，那么△ACD与△BCD的周长差为
如图，直角三角形ABC中，∠C=90°，P，E分别是边AB，BC上的点，D为△ABC外一点，DE⊥BC，DE=EC，BE=2EC，∠BDE=∠PEC，AD∥PE，AC=4，则线段BC的长为