题目内容
(2012•成都模拟)已知关于x、y的方程组
的解是一对异号的数,则k的取值范围是
|
-2<k<1
-2<k<1
.分析:
,先由①-②得3y=6k-6,求出y=2k-2,再把y的值代入②可得到x=k+2,然后利用x与y异号得到
或
,再解不等式组即可得到k的取值范围.
|
|
|
解答:解:
,
①-②得3y=6k-6,
解得y=2k-2③,
把③代入②得x-2k+2=-k+4,
解得x=k+2,
所以方程组的解为
,
∵x与y异号,
∴
或
,
解第一个不等式组得-2<k<1,解第二个不等式组得无解,
所以k的取值范围是-2<k<1.
故答案为-2<k<1.
|
①-②得3y=6k-6,
解得y=2k-2③,
把③代入②得x-2k+2=-k+4,
解得x=k+2,
所以方程组的解为
|
∵x与y异号,
∴
|
|
解第一个不等式组得-2<k<1,解第二个不等式组得无解,
所以k的取值范围是-2<k<1.
故答案为-2<k<1.
点评:本题考查了解二元一次方程组:利用加减消元法或代入消元法把二元一次方程组转化为一元一次方程求解.也考查了不等式组的解法.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 (2012•成都模拟)设函数y=x2-(2k+1)x+2k-4的图象如图所示,它与x轴交于A,B两点,且线段OA与OB的长度之比为1:3,则k=
(2012•成都模拟)设函数y=x2-(2k+1)x+2k-4的图象如图所示,它与x轴交于A,B两点,且线段OA与OB的长度之比为1:3,则k=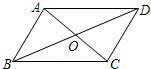 (2012•成都模拟)如图,已知?ABCD的对角线BD=4cm,将?ABCD绕其对称中心O旋转180°,则点D所转过的路径长为( )
(2012•成都模拟)如图,已知?ABCD的对角线BD=4cm,将?ABCD绕其对称中心O旋转180°,则点D所转过的路径长为( )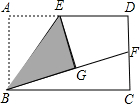 (2012•成都模拟)如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,再延长BG交DC于点F.
(2012•成都模拟)如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,再延长BG交DC于点F.