Question

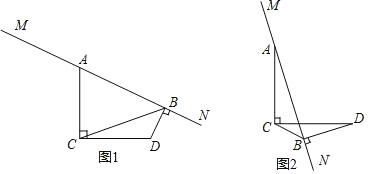
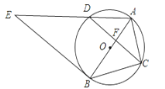
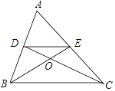
【题目】如图1，菱形纸片ABCD的边长为2，∠ABC=60°，将菱形ABCD沿EF，GH折叠，使得点B，D两点重合于对角线BD上一点P（如图2），则六边形AEFCHG面积的最大值是（ ）

A. B. C. 2﹣ D. 1+

Answer 1

【答案】A

【解析】

由六边形AEFCHG面积＝菱形ABCD的面积﹣△EBF的面积﹣△GDH的面积．得出函数关系式，进而求出最大值．

六边形AEFCHG面积＝菱形ABCD的面积﹣△EBF的面积﹣△GDH的面积．

∵菱形纸片ABCD的边长为2，∠ABC＝60°，∴AC＝2，∴BD＝2，∴S菱形ABCDACBD2×2，设AE＝x，则六边形AEFCHG面积＝2（2﹣x）（2﹣x）xx

x2

（x﹣1）2，∴六边形AEFCHG面积的最大值是．

故选A．