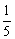题目内容
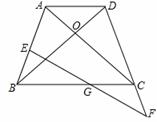
如图,在四边形ABCD中,AD<BC,对角线AC、BD相交于O点,AC=BD,∠ACB=∠DBC.
(1)求证:四边形ABCD为等腰梯形.
(2)若E为AB上一点,延长DC至F,使CF=BE,连接EF 交BC于G,请判断G点是否为EF中点,并说明理由. (改编)
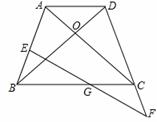
(1)证明:∵∠ACB=∠DBC,∴OB=OC,
∵AC=BD,∴OA=OD,∴∠OAD=∠ODA,
 ∵∠DOC=∠OAD+∠ODA=∠OBC+∠OCB,
∵∠DOC=∠OAD+∠ODA=∠OBC+∠OCB,
∴2∠OAD=2∠OCB,∴∠OAD=∠OCB,∴AD∥BC
∵AD<BC,∴四边形ABCD为梯形.(2分)
在△ABC和△DCB中:AC=BD,∠ACB=∠DBC,CB=BC.
∴△ABC≌△DCB,∴AB=CD,(2分)∴四边形ABCD为等腰梯形.(1分)
(2)解:点G是EF中点.(1分)理由:
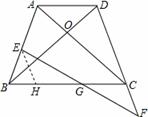 过E作EH∥CD交BC于H.∴∠EHB=∠DCB,∠EHG=∠GCF,
过E作EH∥CD交BC于H.∴∠EHB=∠DCB,∠EHG=∠GCF,
∵梯形ABCD为等腰梯形,∴∠EBH=∠DCB,
∴∠EBH=∠EHB,∴EB=EH,(2分)
∵EB=CF,∴EH=CF,
在△EHG和△FGC中:∠EHG=∠FCG,∠EGH=∠FGC,EH=CF,
∴△EHG≌△FGC,∴EG=FG即G为EF中点.(2分)

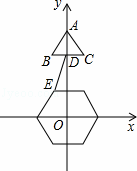
如图,已知边长为2的正三角形ABC顶点A的坐标为(0,6),BC的中点D在y轴上,且在点A下方,点E是边长为2,中心在原点的正六边形的一个顶点,把这个正六边形绕中心旋转一周,在此过程中DE的最小值为( )(改编)
| A. | 4 | B. | 4﹣ | C. | 3 | D. | 6﹣2 |
小明家今年种植的“红灯”樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图象,日销售量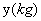 与上市时间
与上市时间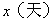 的函数关系如图1所示,樱桃价格
的函数关系如图1所示,樱桃价格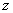 (元/
(元/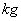 )与上市时间
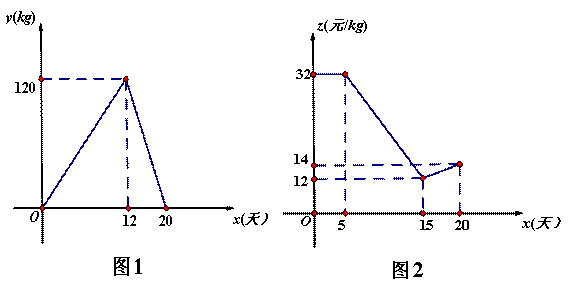
)与上市时间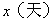 的函数关系式如图2所示。
的函数关系式如图2所示。
 |
(1)求小明家樱桃的日销售量y与上市时间x的函数解析式。
(2)求当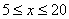 时,樱桃的价格z与上市时间x的函数解析式。
时,樱桃的价格z与上市时间x的函数解析式。
(3)求哪一天的销售金额达到最大,最大值是多少?
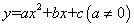 与
与 轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a,b,c]称为“抛物线三角形系数”.
轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a,b,c]称为“抛物线三角形系数”.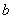 的值;
的值;


 B.
B.  C.
C.  D.
D.
 与直线
与直线 相交于点
相交于点 .直线
.直线 与y轴交于点A.一动点
与y轴交于点A.一动点 从点A出发,先沿平行于x轴的方向运动,到达直线
从点A出发,先沿平行于x轴的方向运动,到达直线 上的点
上的点 处后,改为垂直于x轴的方向运动,到达直线
处后,改为垂直于x轴的方向运动,到达直线 处后,再沿平行于x轴的方向运动,到达直线
处后,再沿平行于x轴的方向运动,到达直线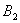 处后,又改为垂直于x轴的方向运动,到达直线
处后,又改为垂直于x轴的方向运动,到达直线 处后,仍沿平行于x轴的方向运动,…… 照此规律运动,动点
处后,仍沿平行于x轴的方向运动,…… 照此规律运动,动点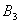 ,
, ,…,
,…, ,
, ,…
,… B.
B. C.
C. D.
D.

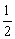 (B)
(B) (C)
(C)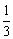 (D)
(D)