��Ŀ����
����Ŀ��ijС��Ϊ���̻��������ƻ������ι���![]() ��
��![]() ���ֻ��ݣ���һ�ηֱ�
���ֻ��ݣ���һ�ηֱ�![]() ��
��![]() ���ֻ���
���ֻ���![]() �ú�
�ú�![]() �ã�������
�ã�������![]() Ԫ���ڶ��ηֱ�
Ԫ���ڶ��ηֱ�![]() ��
��![]() ���ֻ���
���ֻ���![]() �ú�
�ú�![]() �ã����ι�����
�ã����ι�����![]() Ԫ�����ι�����
Ԫ�����ι�����![]() ��
��![]() ���ֻ��ݼ۸���ֱ���ͬ����
���ֻ��ݼ۸���ֱ���ͬ����
��![]() ��
��![]() ��
��![]() ���ֻ���ÿ�õļ۸�ֱ��Ƕ���Ԫ��
���ֻ���ÿ�õļ۸�ֱ��Ƕ���Ԫ��
��![]() ��������
��������![]() ��
��![]() ���ֻ��ݹ�
���ֻ��ݹ�![]() �ã���
�ã���![]() �ֻ��ݵ���������
�ֻ��ݵ���������![]() �ֻ��ݵ�������
�ֻ��ݵ�������![]() �����������һ�ַ�����ʡ�ķ�����������÷���������ã�
�����������һ�ַ�����ʡ�ķ�����������÷���������ã�
���𰸡���![]() ��A��B���ֻ��ݼ۸�ֱ�Ϊ20Ԫ��5Ԫ��
��A��B���ֻ��ݼ۸�ֱ�Ϊ20Ԫ��5Ԫ��
��![]() ��������ʡ�ķ���Ϊ����A�ֻ���11�ã�����B�ֻ���20�ã���������Ϊ320Ԫ��
��������ʡ�ķ���Ϊ����A�ֻ���11�ã�����B�ֻ���20�ã���������Ϊ320Ԫ��
�������������������1����A�ֻ���ÿ�õļ۸�xԪ��B�ֻ���ÿ�õļ۸�yԪ�����ݵ�һ�ηֱ�A��B���ֻ���30�ú�15�ã�������940Ԫ���ڶ��ηֱ�A��B���ֻ���12�ú�5�ã����ι�����675Ԫ���г������飬���ɽ�𣮣�2����A�ֻ��ݵ�����Ϊm�꣬��B�ֻ��ݵ�����Ϊ��31-m���꣬����B�ֻ��ݵ���������A�ֻ��ݵ�������2�����ó�m�ķ�Χ�����ܷ���ΪWԪ�������ܷ���=���ֻ��ݵķ���֮�ͽ���������ϵʽ����һ�κ��������ʾͿ���������ۣ�
�����������![]() ����
����![]() ��
�� ![]() ���ֻ���ÿ�õļ۸�ֱ�Ϊ
���ֻ���ÿ�õļ۸�ֱ�Ϊ![]() Ԫ��
Ԫ��![]() Ԫ��
Ԫ��
�������![]() ��
��
��ã� ![]() ��
��
�� ![]() ��
�� ![]() ���ֻ��ݼ۸�ֱ�Ϊ
���ֻ��ݼ۸�ֱ�Ϊ![]() Ԫ��
Ԫ��![]() Ԫ��
Ԫ��
��![]() ���蹺��
���蹺��![]() �ֻ���
�ֻ���![]() �ã�����
�ã�����![]() �ֻ���Ϊ
�ֻ���Ϊ![]() �ã�
�ã�
�������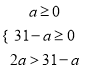 ����
����![]() ������
������
��ã� ![]() ��
��![]() ������
������
�ɣ�![]() ����֪��
����֪�� ![]() �ļ۸�Ϊ
�ļ۸�Ϊ![]() Ԫ/�ã�
Ԫ/�ã� ![]() �ļ۸�Ϊ
�ļ۸�Ϊ![]() Ԫ/�ã�
Ԫ/�ã�
�����Ϊ![]() ��
��
��![]() ��
��
��һ�κ��������ʿɵã� ![]() ��
��![]() �����������
�����������
�൱![]() ȡ��С����
ȡ��С����![]() ʱ����СֵΪ��
ʱ����СֵΪ�� ![]() ��
��
�𣺷�����ʡ�ķ���Ϊ����![]() �ֻ���
�ֻ���![]() �ã�����
�ã�����![]() �ֻ���
�ֻ���![]() �ã���������Ϊ
�ã���������Ϊ![]() Ԫ��
Ԫ��