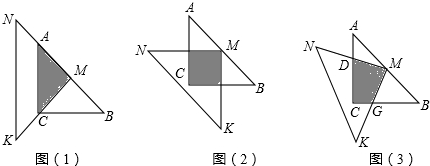
题目内容
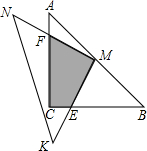
(12分)一位同学拿了两块45º三角尺△MNK和△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=4.
⑴如图1,两三角尺的重叠部分为△ACM,则重叠部分的面积为______,周长为______.
⑵将图1中的△MNK绕顶点M逆时针旋转45º,得到图2,此时重叠部分的面积为____________,周长为____________.
⑶如果将△MNK绕M旋转到不同于图1和图2的图形,如图(3),请你猜想此时重叠部分的面积为___________.
⑷在图3的情况下,若AD=1,求出重叠部分图形的周长.
(1)4; (2)4;8 (3)4 (4)
(2)4;8 (3)4 (4)
解析试题分析:(1) ,
, ,所以
,所以 ,
,
(2)阴影部分的正方形边长为 ,则
,则 ,
,
(3)
如图,做ME⊥AC,MF⊥BC,又 ,
, ,所以
,所以 ,所以
,所以 ,又
,又 ,所以△DME≌△GMF,所以阴影部分面积实际上是正方形EMFC的面积,即面积为4
,所以△DME≌△GMF,所以阴影部分面积实际上是正方形EMFC的面积,即面积为4
(4)根据(3)的结论可知, ,因为
,因为 ,所以
,所以 ,
, ,
, ,所以
,所以 ,
, ,所以
,所以 ,所以阴影部分的周长为
,所以阴影部分的周长为
考点:阴影面积、周长的计算
点评:本题通过将阴影部分拆分重组,可以求出复杂几何的面积、周长,学生需要多做此类题目,掌握好规律,以求举一反三

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
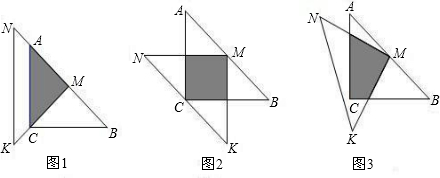
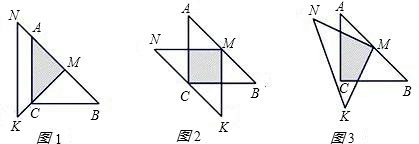
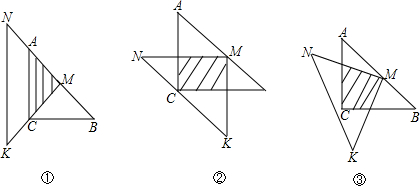
 如图所示,一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动;将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.
如图所示,一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动;将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.