题目内容
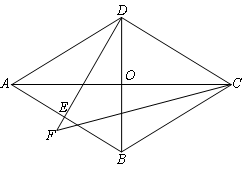
如图,已知正方形ABCD的边长是2,E是AB的中点,延长BC到点F使CF=AE.
(1)求证: ≌
≌ .
.
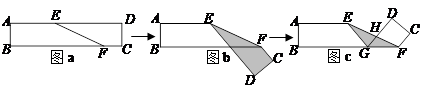
(2)把 向左平移,使
向左平移,使 与
与 重合,得
重合,得 ,
, 交
交 于点
于点 .请判断AH与ED的位置关系,并说明理由.
.请判断AH与ED的位置关系,并说明理由.
(3)求 的长.
的长.

(1)求证:
 ≌
≌ .
.(2)把
 向左平移,使
向左平移,使 与
与 重合,得
重合,得 ,
, 交
交 于点
于点 .请判断AH与ED的位置关系,并说明理由.
.请判断AH与ED的位置关系,并说明理由.(3)求
 的长.
的长.
(1)证明见解析;(2)AH⊥ED.(3) .
.
 .
.试题分析:(1)根据正方形的性质推出∠DAB=∠DCB=90°,AD=DC,根据SAS即可证出答案;
(2)AH⊥ED,根据正方形的性质和平移的性质可证明△ADE≌△CDF,所以得到∠EDF=90°.再由已知条件AH∥DF,利用平行线的性质可证明∠EGH=90°,即垂直成立.
(3)利用勾股定理求出DE的长,再根据三角形的面积公式表示出△EAD的面积即
 AE•AD或
AE•AD或 ED•AG,由已知数据即可求出AG的长.
ED•AG,由已知数据即可求出AG的长.试题解析:(1)证明:∵正方形ABCD,
∴∠DAB=∠DCB=90°,AD=DC,
∴∠DCF=90°=∠DAE,
∵CF=AE,
∴△ADE≌△CDF.
(2)证明:∵正方形ABCD,
∴AB=BC=AD,∠DAB=∠B=90°,
∵E为AB中点,H为BC的中点,
∴AE=BH,
∴△DAE≌△ABH,
∴∠EDA=∠BAH,
∵∠AED+∠ADE=90°,
∴∠AED+∠BAH=90°,
∴∠AGE=180°-90°=90°,
∴AH⊥ED.
(3)在△EAD中,由勾股定理得:DE=
 ,
,由三角形的面积公式得:AE×AD=DE×AG,
∴1×2=
 ×AG,
×AG,∴AG=
 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




 ,tan37°=
,tan37°=

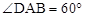 ,DF⊥AB于点E,且DF=DC,连接FC,则∠ACF的度数为 度.
,DF⊥AB于点E,且DF=DC,连接FC,则∠ACF的度数为 度.