题目内容
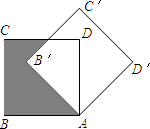如图，已知正方形ABCD的边长为a，将正方形ABCD绕点A顺时针旋转45°，则阴影部分的面积为
- A.
a2 - B.（2-
）a2 - C.
a2 - D.（
-1）a2
B
分析：连接B′C，根据正方形的对角线平分一组对角可知AB′在正方形ABCD的对角线上，设B′C′交CD于E，根据正方形的对角线等于边长的倍求出AC，然后求出B′C，然后根据阴影部分的面积等于两个等腰直角三角形的面积，列式进行计算即可得解．
解答：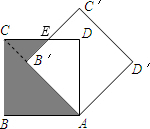
解：如图，连接B′C，
∵旋转角为45°，正方形的对角线平分一组对角，
∴AB′在正方形ABCD的对角线上，
设B′C′交CD于E，
∵正方形ABCD的边长为a，
∴AC=a，B′C=a-a，
∴阴影部分的面积=
a•a+（a-a）×（a-a）=a2+（a-a）2，
=（2-）a2．
故选B．
点评：本题考查了旋转的性质，正方形的性质，根据旋转角为45°判断出AB′在正方形ABCD的对角线上是解题的关键．
分析：连接B′C，根据正方形的对角线平分一组对角可知AB′在正方形ABCD的对角线上，设B′C′交CD于E，根据正方形的对角线等于边长的
倍求出AC，然后求出B′C，然后根据阴影部分的面积等于两个等腰直角三角形的面积，列式进行计算即可得解．解答：
解：如图，连接B′C，∵旋转角为45°，正方形的对角线平分一组对角，
∴AB′在正方形ABCD的对角线上，
设B′C′交CD于E，
∵正方形ABCD的边长为a，
∴AC=
a，B′C=a-a，∴阴影部分的面积=
a•a+（a-a）×（a-a）=a2+（a-a）2，=（2-
）a2．故选B．
点评：本题考查了旋转的性质，正方形的性质，根据旋转角为45°判断出AB′在正方形ABCD的对角线上是解题的关键．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
如图，已知正方形ABCD的边AB与正方形AEFM的边AM在同一直线上，直线BE与DM交于点N．求证：BN⊥DM．
（2013•北碚区模拟）如图，已知正方形ABCD，点E是BC上一点，点F是CD延长线上一点，连接EF，若BE=DF，点P是EF的中点．
如图，已知正方形ABCD，点E在BC边上，将△DCE绕某点G旋转得到△CBF，点F恰好在AB边上．
如图，已知正方形ABCD的对角线交于O，过O点作OE⊥OF，分别交AB、BC于E、F，若AE=4，CF=3，则EF的值是（ ）
如图，已知正方形ABCD的对角线AC，BD相交于点O，E是AC上的一点，过点A作AG⊥BE，垂足为G，AG交BD于点F．