题目内容
如图,一架飞机以每小时900千米的速度水平飞行,某个时刻,从地面控制塔O(塔高300m)观测到飞机在A处的仰角为30°,5分钟后测得飞机在B处的仰角为45°,试确定飞机的飞行高度.(
=1.732,结果精确到0.1km).
| 3 |


由题意得:AB=900×
| 5 |
| 60 |
过点O作OD⊥AB,垂足为D,
设OD=x千米,在Rt△OBD中,
∵∠OBD=45°,
∴BD=OD=x千米,
在Rt△OAD中,AD=AB+BD=(x+75)千米,∠AOD=60°,
∵tan∠AOD=
| AD |
| OD |
∴
| x+75 |
| x |
| 3 |
解得x=102.45,
∴CD=OD+OC=102.45+0.3=102.75≈102.8(km),
答:飞机的飞行高度约为102.8km.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•成都一模)如图,一架飞机以每小时900千米的速度水平飞行,某个时刻,从地面控制塔O(塔高300m)观测到飞机在A处的仰角为30°,5分钟后测得飞机在B处的仰角为45°,试确定飞机的飞行高度.(
(2013•成都一模)如图,一架飞机以每小时900千米的速度水平飞行,某个时刻,从地面控制塔O(塔高300m)观测到飞机在A处的仰角为30°,5分钟后测得飞机在B处的仰角为45°,试确定飞机的飞行高度.( 如图,一架飞机以每小时900千米的速度水平飞行,某个时刻,从地面控制塔O(塔高300m)观测到飞机在A处的仰角为30°,5分钟后测得飞机在B处的仰角为45°,试确定飞机的飞行高度.(
如图,一架飞机以每小时900千米的速度水平飞行,某个时刻,从地面控制塔O(塔高300m)观测到飞机在A处的仰角为30°,5分钟后测得飞机在B处的仰角为45°,试确定飞机的飞行高度.(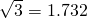 ,结果精确到0.1km).
,结果精确到0.1km). ,结果精确到0.1km).
,结果精确到0.1km).
 ,结果精确到0.1km).
,结果精确到0.1km).