题目内容
如图,在⊙O中,直径MN=10,正方形ABCD的四个顶点都分别在半径OP、OM及⊙O上,且∠POM=45º,则AB=( )

A.2
B. C.
C. D.
D.
【答案】
B.
【解析】
试题分析: ∵ABCD是正方形,∴∠DCO=90°,∵∠POM=45°,∴∠CDO=45°,∴CD=CO,
∴BO=BC+CO=BC+CD,∴BO=2AB,连接AO,∵MN=10,∴AO=5,在Rt△ABO中,AB2+BO2=AO2,AB2+(2AB)2=52,解得:AB= ,则AB的长为
,则AB的长为 .故选B.
.故选B.

考点:1.正方形的性质;2.勾股定理;3.圆的认识.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
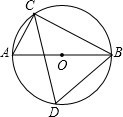 如图,在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,则BC=
如图,在⊙O中,直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D,则BC=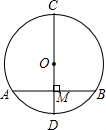 如图,在⊙O中,直径CD的长度为10cm,AB是弦,且AB⊥CD于M,OM=3cm,求弦AB的长.
如图,在⊙O中,直径CD的长度为10cm,AB是弦,且AB⊥CD于M,OM=3cm,求弦AB的长.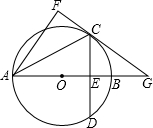 C与直线AB相交于点G.
C与直线AB相交于点G. (2013•百色)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( )
(2013•百色)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( ) (2012•朝阳区二模)如图,在⊙O中,直径AB⊥弦CD于点H,E是⊙O上的点,若∠BEC=25°,则∠BAD的度数为( )
(2012•朝阳区二模)如图,在⊙O中,直径AB⊥弦CD于点H,E是⊙O上的点,若∠BEC=25°,则∠BAD的度数为( )