题目内容
如图所示,四边形OABC是矩形,点D在OC边上,以AD为折痕,将△OAD向上翻折,点O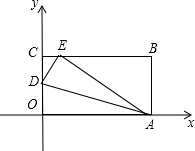 恰好落在BC边上的点E处,若△ECD的周长为2,△EBA的周长为6.
恰好落在BC边上的点E处,若△ECD的周长为2,△EBA的周长为6.
(1)矩形OABC的周长为______;
(2)若A点坐标为 ,求线段AE所在直线的解析式.
,求线段AE所在直线的解析式.
解:(1)∵DE=DO,EA=OA,
∴矩形OABC的周长=△ECD的周长+△EBA的周长.
∴矩形OABC的周长为8.
(2)∵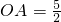 ,
,
∴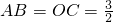 .
.
∴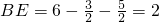 .
.
∴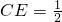 ,即点E的坐标为
,即点E的坐标为
设直线AE的解析式为y=kx+b,
则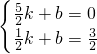 ,解得
,解得
∴直线AE的解析式为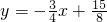 .
.
分析:(1)由折叠的意义,△ECD的周长与△EBA的周长之和等于矩形OABC的周长,
(2)根据A点坐标为 ,求出OC的长,再求出E点的横坐标,从而得到线段AE所在直线的解析式.
,求出OC的长,再求出E点的横坐标,从而得到线段AE所在直线的解析式.
点评:本题是函数与三角形相结合的问题,同时又考查了矩形的性质,是一道中难度题.
∴矩形OABC的周长=△ECD的周长+△EBA的周长.
∴矩形OABC的周长为8.
(2)∵
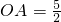 ,
,∴
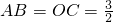 .
.∴
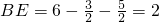 .
.∴
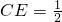 ,即点E的坐标为
,即点E的坐标为
设直线AE的解析式为y=kx+b,
则
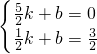 ,解得
,解得
∴直线AE的解析式为
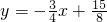 .
.分析:(1)由折叠的意义,△ECD的周长与△EBA的周长之和等于矩形OABC的周长,
(2)根据A点坐标为
 ,求出OC的长,再求出E点的横坐标,从而得到线段AE所在直线的解析式.
,求出OC的长,再求出E点的横坐标,从而得到线段AE所在直线的解析式.点评:本题是函数与三角形相结合的问题,同时又考查了矩形的性质,是一道中难度题.

练习册系列答案
相关题目
 如图所示,四边形OABC为正方形,边长为6,点A,C分别在x轴,y轴的正半轴上,点D在OA上,且D的坐标为(2,0),P是OB上的一动点,试求PD+PA和的最小值是( )
如图所示,四边形OABC为正方形,边长为6,点A,C分别在x轴,y轴的正半轴上,点D在OA上,且D的坐标为(2,0),P是OB上的一动点,试求PD+PA和的最小值是( ) 端点B、C不重合),过点D作直线y=-
端点B、C不重合),过点D作直线y=- (2013•吴中区一模)如图所示,四边形OABC是矩形,点A、C的坐标分别为(6,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-
(2013•吴中区一模)如图所示,四边形OABC是矩形,点A、C的坐标分别为(6,0),(0,2),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=-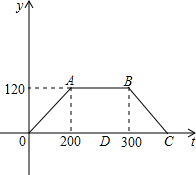 小明参加汽车驾驶培训,在实际操作考试时,被要求进行启动加速、匀速运行、制动减速三个连贯过程,在加速和减速运动过程中,路程和速度均满足关系s=
小明参加汽车驾驶培训,在实际操作考试时,被要求进行启动加速、匀速运行、制动减速三个连贯过程,在加速和减速运动过程中,路程和速度均满足关系s= 如图所示,四边形ABCD与A′B′C′D′以0为位似中心,位似比为1:2.则点A的对应点是点
如图所示,四边形ABCD与A′B′C′D′以0为位似中心,位似比为1:2.则点A的对应点是点