题目内容
【题目】小李想用篱笆围成一个周长为60米的矩形场地,矩形面积S(单位:平方米)随矩形一边长x(单位:米)的变化而变化.
(1)求S与x之间的函数关系式,并写出自变量x的取值范围;
(2)当x是多少时,矩形场地面积S最大,最大面积是多少?
【答案】
(1)解:S=x(30﹣x)
自变量x的取值范围为:
0<x<30
(2)解:S=x(30﹣x)
=﹣(x﹣15)2+225,
∴当x=15时,S有最大值为225平方米.
即当x是15时,矩形场地面积S最大,最大面积是225平方米
【解析】(1)已知周长为60米,一边长为x,则另一边长为30﹣x.(2)用配方法化简函数解析式,求出s的最大值.

练习册系列答案
相关题目
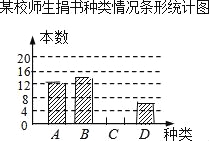
【题目】在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题:
某校师生捐书种类情况统计表
种类 | 频数 | 百分比 |
A.科普类 | 12 | n |
B.文学类 | 14 | 35% |
C.艺术类 | m | 20% |
D.其它类 | 6 | 15% |
(1)统计表中的m= ,n= ;
(2)补全条形统计图;
(3)本次活动师生共捐书2000本,请估计有多少本科普类图书?