题目内容
一个圆锥的侧面展开图是一个圆心角为216°，面积为60π的扇形，则这个圆锥的高是________．
8
分析：首先利用扇形面积公式求出扇形的半径，进而求出底面圆的半径，再利用勾股定理求出圆锥的高即可．
解答：设母线长为r，底面圆的半径为R，
S扇形=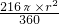
=60π，
解得：r=10，
底面圆的周长为：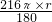
=12π=2πR，
解得：R=6，
∴这个圆锥的高是：
=8．
故答案为：8．
点评：本题考查了圆锥的计算，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键．
分析：首先利用扇形面积公式求出扇形的半径，进而求出底面圆的半径，再利用勾股定理求出圆锥的高即可．
解答：设母线长为r，底面圆的半径为R，
S扇形=
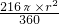=60π，解得：r=10，
底面圆的周长为：
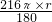=12π=2πR，解得：R=6，
∴这个圆锥的高是：
=8．故答案为：8．
点评：本题考查了圆锥的计算，正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
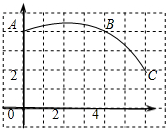如图，在正方形网格图中建立一直角坐标系，一条圆弧经过网格点A、B、C，请在网格中进行下列操作：
（2013•本溪二模）一个圆锥的侧面展开图是半径为1的半圆，则该圆锥的底面半径是
如图，一个圆锥的侧面展开图是90°的扇形．
如图，在单位长度为1的正方形网格中建立平面直角坐标系，一段圆弧经过网格的交点为A、B、C．