Question

【题目】已知直线与轴，轴分别交于点，将对折，使点的对称点落在直线上，折痕交轴于点．

（1）求点的坐标；

（2）若已知第四象限内的点，在直线上是否存在点，使得四边形为平行四边形？若存在，求出点的坐标；若不存在，说明理由；

（3）设经过点且与轴垂直的直线与直线的交点为为线段上一点，求的取值范围．

Answer 1

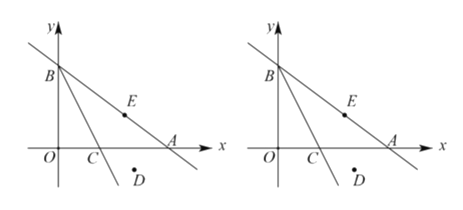
【答案】（1）C（3，0）；（2）不存在；（3）0≤|QAQO|≤4．

【解析】

（1）由勾股定理得：CA2＝CE2＋AE2，即（8a）2＝a2＋42，即可求解；

（2）当四边形OPAD为平行四边形时，根据OA的中点即为PD的中点即可求解；

（3）当点Q为AO的垂直平分线与直线BC的交点时，QO＝QA，则|QAQO|＝0，当点Q在点B处时，|QAQO|有最大值，即可求解．

解：（1）连接CE，则CE⊥AB，

与x轴，y轴分别相交于点A，B，

则点A、B的坐标分别为：（8，0）、（0，6），则AB＝10，

设：OC＝a，则CE＝a，BE＝OB＝6，

AE＝106＝4，CA＝8a，

由勾股定理得：CA2＝CE2＋AE2，即（8a）2＝a2＋42，

解得a＝3，

故点C（3，0）；

（2）不存在，理由：

将点B、C的坐标代入一次函数表达式y＝kx＋b并解得：

直线BC的表达式为：y＝2x＋6，

设点P（m，n），当四边形OPAD为平行四边形时，

OA的中点即为PD的中点，

即：m＋＝8，n＝0，

解得：m＝，n＝，

当x＝时，y＝2x＋6＝1，

故点P不在直线BC上，

即在直线BC上不存在点P，使得四边形OPAD为平行四边形；

（3）当x＝时，y＝2x＋6＝5，故点F（，5），

当点Q为AO的垂直平分线与直线BC的交点时，QO＝QA，

则|QAQO|＝0，

当点Q在点B处时，|QAQO|有最大值，

此时：点A（8，0）、点O（0，0）、点Q（0，6），

则AQ＝10，QO＝6，|QAQO|＝4，

故|QAQO|的取值范围为：0≤|QAQO|≤4．