Question

阅读下面的材料：

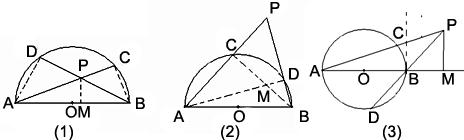
如图（1），在以AB为直径的半圆O内有一点P，AP、BP的延长线分别交半圆O于点C、D．

求证：AP?AC+BP?BD=AB²．

证明：连结AD、BC，过P作PM⊥AB，则∠ADB=∠AMP=90^ｏ，

∴点D、M在以AP为直径的圆上；同理：M、C在以BP为直径的圆上．

由割线定理得： AP?AC=AM?AB，BP?BD=BM?BA，

所以，AP?AC+BP?BD=AM?AB+BM?AB=AB?（AM+BM）=AB²．

　当点P在半圆周上时，也有AP?AC+BP?BD=AP²+BP²=AB²成立，那么：

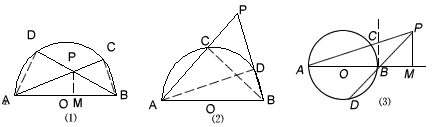
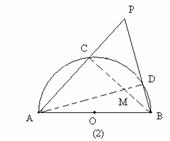
（1）如图（2）当点P在半圆周外时，结论AP?AC+BP?BD=AB²是否成立？为什么？

（2）如图（3）当点P在切线BE外侧时，你能得到什么结论？将你得到的结论写出来．

Answer 1

解：（1）成立．                       

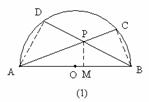
 证明：如图（2），∵∠PCM=∠PDM=90⁰，

∴点C、D在以PM为直径的圆上，

∴AC?AP=AM?MD，BD?BP=BM?BC，

∴AC?AP+BD?BP=AM?MD+BM?BC，

由已知，AM?MD+BM?BC=AB²，

∴AP?AC+BP?BD=AB²．

（2）如图（3），过P作PM⊥AB，交AB的延长线于M，连结AD、BC，

则C、M在以PB为直径的圆上，∴AP?AC=AB?AM，①

D、M在以PA为直径的圆上，∴BP?BD=AB?BM，②       

由图像可知：AB=AM-BM，③

由①②③可得：AP?AC-BP?BD=AB?（AM-BM）=AB²．