题目内容
抛物线y=x2-4x+3的顶点及它与x轴的交点三点连线所围成的三角形面积是 .
【答案】分析:抛物线y=x2-4x+3的顶点及它与x轴的交点三点连线所围成的三角形中:底边长为与x轴的两交点之间的距离,高为抛物线的顶点的纵坐标的绝对值,再利用三角形的面积公式即可求出b的值.
解答:解:由题意可得:抛物线的顶点的纵坐标为 =-1,
=-1,
∴底边上的高为1;
∵x2-4x+3=0,解得x1=1,x2=3,
∴抛物线与x轴的交点为(1,0)、(3,0);
由题意得:底边长=|x1-x2|=2,
∴抛物线y=x2-4x+3的顶点及它与x轴的交点三点连线所围成的三角形面积为: ×2×1=1.
×2×1=1.
点评:要求熟悉二次函数与一元二次方程的关系和坐标轴上两点距离公式|x1-x2|,并能与几何知识结合使用.
解答:解:由题意可得:抛物线的顶点的纵坐标为
 =-1,
=-1,∴底边上的高为1;
∵x2-4x+3=0,解得x1=1,x2=3,
∴抛物线与x轴的交点为(1,0)、(3,0);
由题意得:底边长=|x1-x2|=2,
∴抛物线y=x2-4x+3的顶点及它与x轴的交点三点连线所围成的三角形面积为:
 ×2×1=1.
×2×1=1.点评:要求熟悉二次函数与一元二次方程的关系和坐标轴上两点距离公式|x1-x2|,并能与几何知识结合使用.

练习册系列答案
相关题目
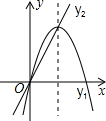 如图,抛物线y1=-x2+4x和直线y2=2x.当y1>y2时,x的取值范围是( )
如图,抛物线y1=-x2+4x和直线y2=2x.当y1>y2时,x的取值范围是( )| A、0<x<2 | B、x<0或x>2 | C、x<0或x>4 | D、0<x<4 |