题目内容
已知二次函数y=ax2-5x+c的图象如图所示,请根据图象回答下列问题:

(1) a=_______,c=______.
(2)函数图象的对称轴是_________,顶点坐标P__________.
(3)该函数有最______值,当x=______时,y最值=________.
(4)当x_____时,y随x的增大而减小.当x_____时,y随x的增大而增大.
(5)抛物线与x轴交点坐标A_______,B________;与y轴交点C 的坐标为_______; =_________,
=_________, =________.
=________.
(6)当y>0时,x的取值范围是_________;当y<0时,x的取值范围是_________.
(7)方程ax2-5x+c=0中△的符号为________.方程ax2-5x+c=0的两根分别为_____,____.
(8)当x=6时,y______0;当x=-2时,y______0.
(1)a=1;c=4 (2)直线x= ,
, (3)小;
(3)小;  ;
; (4)
(4) (5)(1,0);(4,0);(0,4); 6;
(5)(1,0);(4,0);(0,4); 6;  ; (6)x<1或x>4;1<x<4
(7)正号;x1=1;x2=4 (8)>;>
; (6)x<1或x>4;1<x<4
(7)正号;x1=1;x2=4 (8)>;>
【解析】本题全面考查了二次函数的性质
根据函数图象可知,抛物线与x轴交于A、B两点,将两点代入函数求得解析式,再根据函数的性质将各小题补充完整.
解:(1)由A(1,0)、B(4,0)代入函数可解得:a=1,c=4;
(2)将解得的函数y=x2-5x+4变形得:y=(x- )2-
)2- ,则对称轴x=
,则对称轴x= ,顶点坐标(
,顶点坐标( ,-
,- );
);
(3)小、 、-
、- ;
;
(4)≤ 、≥
、≥ ;
;
(5)(1,0)、(4,0)、(0,4)、6、
(6)x<1或x>4、1<x<4;
(7)正号、x1=1、x2=4;
(8)>、>.

 口算题天天练系列答案
口算题天天练系列答案已知二次函数y=ax+bx+c(a≠0,a,b,c为常数),对称轴为直线x=1,它的部分自变量与函数值y的对应值如下表,写出方程ax2+bx+c=0的一个正数解的近似值________(精确到0.1).
| x | -0.1 | -0.2 | -0.3 | -0.4 |
| y=ax2+bx+c | -0.58 | -0.12 | 0.38 | 0.92 |
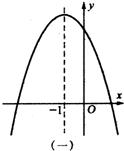 21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
