题目内容
若二次函数y=ax2+bx+c经过（-4，1），（2，1）两点，则它的对称轴是
- A.直线x=-
- B.直线x=1
- C.直线x=-1
- D.不能确定
C
分析：由（-4，1），（2，1）两点的坐标特点得到这两点的连线平行于x轴，于是这两点关于二次函数的对称轴对称，则这两点的连线的垂直平分线x=-1即为二次函数的对称轴．
解答：∵（-4，1），（2，1）两点的纵坐标相等，
∴这两点的连线平行于x轴，
∴这两点关于二次函数的对称轴对称，
∴二次函数的对称轴是直线x=2-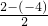
=2-3=-1．
故选C．
点评：本题考查了二次函数的性质：二次函数y=ax2+bx+c的图象是一条抛物线，它为轴对称图形，对称轴为直线x=-
，在对称轴左侧y随着x的增大而增大；在对称轴右侧y随着x的增大而减小．
分析：由（-4，1），（2，1）两点的坐标特点得到这两点的连线平行于x轴，于是这两点关于二次函数的对称轴对称，则这两点的连线的垂直平分线x=-1即为二次函数的对称轴．
解答：∵（-4，1），（2，1）两点的纵坐标相等，
∴这两点的连线平行于x轴，
∴这两点关于二次函数的对称轴对称，
∴二次函数的对称轴是直线x=2-
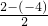=2-3=-1．故选C．
点评：本题考查了二次函数的性质：二次函数y=ax2+bx+c的图象是一条抛物线，它为轴对称图形，对称轴为直线x=-
，在对称轴左侧y随着x的增大而增大；在对称轴右侧y随着x的增大而减小． 
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（1998•大连）若二次函数y=ax2+bx+c（a≠0）的图象如图，则直线y=bx-c不经过（ ）
如图，已知点O为坐标原点，∠AOB=30°，∠B=90°，且点A的坐标为（2，0）．