题目内容
抛物线y=ax2经过点（3，5），则a=
．函数y=
（x2-1）的自变量x的取值范围是
| 5 |
| 9 |
| 5 |
| 9 |
| 3 |
| 4 |
全体实数
全体实数
．分析：把点（3，5）代入抛物线y=ax2求出a的值；根据函数y=
（x2-1）是二次函数即可求出x的取值范围．
| 3 |
| 4 |
解答：解：∵抛物线y=ax2经过点（3，5），
∴5=9a，解得a=
；
∵函数y=
（x2-1）是二次函数，
∴自变量x的取值范围是全体实数．
故答案为：
；全体实数．
∴5=9a，解得a=
| 5 |
| 9 |
∵函数y=
| 3 |
| 4 |
∴自变量x的取值范围是全体实数．
故答案为：
| 5 |
| 9 |
点评：本题考查的是二次函数的性质及二次函数图象上点的坐标特点，解答此题的关键是熟知二次函数图象上各点的坐标一定适合此函数的解析式．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
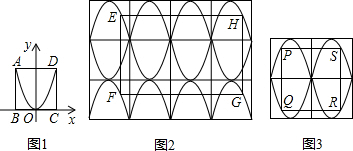及其内部的抛物线部分经过平移和对称变换得到的．
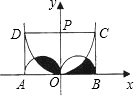如图，矩形ABCD的长AB=6cm，宽AD=3cm．O是AB的中点，OP⊥AB，两半圆的直径分别为AO与OB．抛物线y=ax2经过C、D两点，则图中阴影部分的面积是
如图，矩形ABCD的长AB=8cm，宽AD=3cm．O是AB的中点，OP⊥AB，两半圆的直径分别为AO与OB．抛物线y=ax2经过C、D两点，则用图中阴影部分（整体）围成的圆锥的底面半径的长是