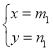题目内容
【题目】对于一个三角形,设其三个内角度数分别为![]() ,
,![]() 和
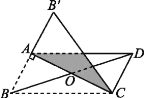
和![]() ,若x,y,z满足
,若x,y,z满足![]() ,我们定义这个三角形为美好三角形.
,我们定义这个三角形为美好三角形.
(1)△ABC中,若![]() ,
,![]() ,则△ABC (填”是”或”不是”)美好三角形;
,则△ABC (填”是”或”不是”)美好三角形;
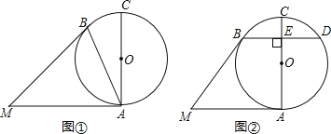
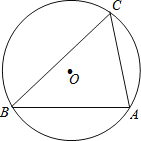
(2)如图,锐角△ABC是⊙O的内接三角形,![]() ,
,![]() ,⊙O直径为
,⊙O直径为![]() ,求证:△ABC为美好三角形;
,求证:△ABC为美好三角形;
(3)已知△ABC为美好三角形,![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)不是;(2)见解析;(3)∠C=78°或72°
【解析】
(1)利用美好三角形的定义得出△ABC的形状进而求出即可;
(2)利用勾股定理的逆定理得出△ABC的形状进而得出答案;
(3)利用美好三角形的定义进而分别得出∠C的度数.
(1)解:∵△ABC中,∠A=40°,∠B=80°,
∴∠C=60°
∵402+602≠802,
∴△ABC不是美好三角形;
故答案为:不是;
(2)证明:连接OA、OC,
∵AC=2,OA=OC=![]() ,
,
∴△OAC是直角三角形,即∠AOC=90°,
∴∠B=45°,
∵∠C=60°,
∴∠A=75°,
∵即三个内角满足关系:452+602=5625=752,
∴△ABC是美好三角形;
(3)解:设∠C=x°,则∠B=(150﹣x)°,
若∠C为最大角,则x2=(150﹣x)2+302,
解得x=78,
若∠B最大角,则(150﹣x)2=x2+302,
解得x=72,
综上可知,∠C=78°或72°

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目