Question

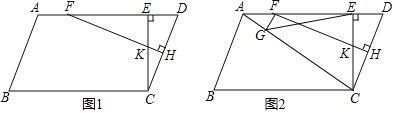
【题目】如图，在正方形ABCD中，点E在对角线BD上，EF∥AB交AD于点F，连接BF．

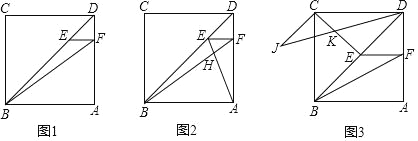
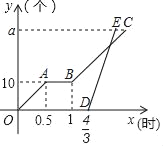
（1）如图1，若AB＝4，DE＝，求BF的长；

（2）如图2．连接AE，交BF于点H，若DF＝HF＝2，求线段AB的长；

（3）如图3，连接BF，AB＝3，设EF＝x，△BEF的面积为S，请用x的表达式表示S，并求出S的最大值；当S取得最大值时，连接CE，线段DB绕点D顺时针旋转30°得到线段DJ，DJ与CE交于点K，连接CJ，求证：CJ⊥CE．

Answer 1

【答案】（1）5；（2）8；（3），，见解析.

【解析】

（1）由正方形的性质可得AB＝AD＝4，∠A＝90°，∠BDA＝45°＝∠DBA，由平行线性质可得∠DFE＝∠A＝90°，∠DEF＝∠DBA＝∠EDF＝45°，可得DF＝1，AF＝3，由勾股定理可求BF的长；

（2）由题意可得DF＝EF＝FH＝2，由平行线的性质和等腰三角形的性质可得∠BAE＝∠FHE＝∠BHA，可得AB＝BH，由勾股定理可求AB的长；

（3）由三角形面积公式可求S△BEF＝EF×AF＝x（3﹣x）＝由二次函数性质可得x＝时，S取得最大值，即点E是BD中点，由旋转的性质和直角三角形的性质可证四边形JCEN是矩形，可证CJ⊥CE．

解：（1）∵四边形ABCD是正方形，

∴AB＝AD＝4，∠A＝90°，∠BDA＝45°＝∠DBA，

∵EF∥AB

∴∠DFE＝∠A＝90°，∠DEF＝∠DBA＝∠EDF＝45°

∴DF＝EF

∴DE＝DF＝

∴DF＝1

∴AF＝AD﹣DF＝3

∴BF＝＝5

（2）∵DF＝EF，DF＝HF＝2，

∴EF＝2＝FH

∴∠FEH＝∠FHE

∵EF∥AB

∴∠FEH＝∠BAE，

∴∠BAE＝∠FHE＝∠BHA

∴AB＝BH

∵在Rt△ABE中，BF2＝AF2+AB2，

∴（AB+2）2＝（AB﹣2）2+AB2，

∴AB＝8，AB＝0（不合题意舍去）

∴AB＝8

（3）如图，过点J作JN⊥BD于，

∵S△BEF＝EF×AF＝x（3﹣x）＝∴当x＝时，S△BEF最大值为，

∵x＝，

∴EF＝

∵EF∥AB

∴

∴BD＝2DE，AD＝2DF

∵CB＝CD，BD＝2DE，

∴CE⊥BD，BD＝2CE，

∵旋转

∴JD＝BD，∠JDB＝30°，

又∵JN⊥BD

∴JD＝2JN，

∴BD＝2JN，

∴JN＝CE，

∵JN⊥BD，CE⊥BD

∴JN∥CE，且CE＝JN

∴四边形JCEN是平行四边形，

∵JN⊥BD

∴四边形JCEN是矩形

∴CJ⊥CE