题目内容
 如图,已知一次函数y=ax+b的图象分别与双曲线y=
如图,已知一次函数y=ax+b的图象分别与双曲线y=| 3 | x |
(1)求一次函数解析式;
(2)求△OAB的面积.
分析:(1)作AG⊥x轴,则AG=1,根据题意可得出点A、M的坐标,从而求出一次函数的解析式;
(2)联立列方程组可得出点B的坐标,则S△AOB=S△OBN+S△MON+S△OAM.
(2)联立列方程组可得出点B的坐标,则S△AOB=S△OBN+S△MON+S△OAM.
解答:解:(1)作AG⊥x轴,则AG=1,
由已知双曲线y=
得A点坐标为(3,1)…(1分)
∵在Rt△OMN中,OM=ON
∴∠ONM=∠OMN=45°从而∠AMG=45°
∴MG=AG=1,得M点坐标为(2,0)…(3分)
由题意得
,
∴
∴一次函数解析式为y=x-2 …(5分)
(2)由
可求得点B坐标为(-1,-3)…(7分)
∴S△AOB=S△OBN+S△MON+S△OAM
=
×1×2+
×2×2+
×1×2
=4 …(9分)
由已知双曲线y=
| 3 |
| x |
∵在Rt△OMN中,OM=ON
∴∠ONM=∠OMN=45°从而∠AMG=45°
∴MG=AG=1,得M点坐标为(2,0)…(3分)
由题意得
|
∴
|
∴一次函数解析式为y=x-2 …(5分)
(2)由
|
∴S△AOB=S△OBN+S△MON+S△OAM
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=4 …(9分)
点评:本题考查了一次函数和反比例函数的交点问题以及用待定系数法求反比例函数和一次函数的解析式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
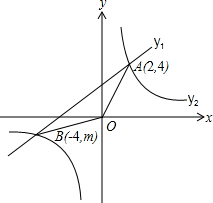 B(-4,m)两点.
B(-4,m)两点. 如图,已知一次函数y=kx+b的图象与反比例函数y=-
如图,已知一次函数y=kx+b的图象与反比例函数y=- (2013•新疆)如图,已知一次函数y1=kx+b与反比例函数
(2013•新疆)如图,已知一次函数y1=kx+b与反比例函数 如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数
如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数 如图,已知一次函数y=kx+b的图象交反比例函数
如图,已知一次函数y=kx+b的图象交反比例函数