题目内容
如图，直线y=2x+4与x轴、y轴分别交于A、B两点，把△OAB绕点O顺时针旋转90°得到△OCD．
【小题1】求经过A、B、D三点的抛物线的解析式
【小题2】点P是第一象限内抛物线上一点，是否存在这样的点P，使得点P到直线CD的距离最大，若存在，请求出点P的坐标；若不存在，请说明理由．
p;【答案】
【小题1】∵直线y=2x+4与x轴、y轴分别交于A、B两点，
∴ A(-2, 0)、B(0, 4). …………1分
∵△OAB绕点O顺时针旋转90°得到△OCD
∴ C(0, 2)、D(4, 0) …………2分
∴ 过A、B、D的抛物线解析式为y= -x2+x+4…………4分
【小题2】∵C(0, 2)、D(4, 0)
∴ 直线CD解析式为y= -x+2…………5分
设P(x, -x2+x+4) (0＜x＜4)…………6分
作PE^x轴于E，交CD于Q,
则E(x, 0), Q(x, -x+2) …………7分
∴PQ=(-x2+x+4)-(-x+2)= -x2+x+2 …………8分
OE=x, DE=4-x
∴S△PCD=S△PCQ+S△PDQ=PQ·OE+PQ·DE=PQ·OD
=(-x2+x+2)×4= -x2+3x+4= - (x-)2+…………9分
∴当x=时，△PCD的面积最大，也即P到CD得距离最大。
∴存在点P，使得点P到直线CD的距离最大，此时P点的坐标为（，）
…………10分解析:
略
【小题1】∵直线y=2x+4与x轴、y轴分别交于A、B两点，
∴ A(-2, 0)、B(0, 4). …………1分
∵△OAB绕点O顺时针旋转90°得到△OCD
∴ C(0, 2)、D(4, 0) …………2分
∴ 过A、B、D的抛物线解析式为y= -x2+x+4…………4分
【小题2】∵C(0, 2)、D(4, 0)
∴ 直线CD解析式为y= -x+2…………5分
设P(x, -x2+x+4) (0＜x＜4)…………6分
作PE^x轴于E，交CD于Q,
则E(x, 0), Q(x, -x+2) …………7分
∴PQ=(-x2+x+4)-(-x+2)= -x2+x+2 …………8分
OE=x, DE=4-x
∴S△PCD=S△PCQ+S△PDQ=PQ·OE+PQ·DE=PQ·OD
=(-x2+x+2)×4= -x2+3x+4= - (x-)2+…………9分
∴当x=时，△PCD的面积最大，也即P到CD得距离最大。
∴存在点P，使得点P到直线CD的距离最大，此时P点的坐标为（，）
…………10分解析:
略
练习册系列答案
阅读快车系列答案
相关题目
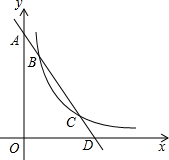如图，直线y=-2x+b与y轴交于点A，与x轴交于点D，与双曲线
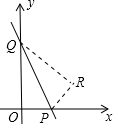如图，直线y=-2x+6与x轴、y轴分别交于P、Q两点，把△POQ沿PQ翻折，点O落在R处，则点R的坐标是
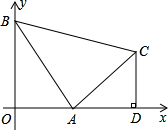腰直角△ABC，∠BAC=90°，过C作CD⊥x轴，垂足为D．
轴分别交于点C、D．直线EB交x轴于点F．
如图，直线y=-2x+8与两坐标轴分别交于P，Q两点，在线段PQ上有一点A，过点A分别作两坐标轴的垂线，垂足分别为B、C．