Question

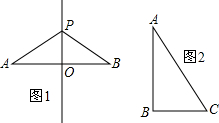
（1）如图1，已知△ABC中，∠BAC=45°，AB=AC，AD⊥BC于D，将△ABC沿AD剪开，并分别以AB、AC为轴翻转，点E、F分别是点D的对应点，得到△ABE和△ACF （与△ABC在同一平面内），延长EB、FC相交于G点，证明四边形AEGF是正方形；
（2）如果（1）中AB≠AC，其他不变，如图2，那么四边形AEGF是否是正方形？请说明理由；
（3）在（2）中，若BD=2，DC=3，求AD的长。

                        图1                                             图2

Answer 1

解：（1）∵，AB=AC，∠ADB=∠ADC=90°，AD=AD，
∴△ADB≌△ADC，
∴∠DAB=∠DAC=∠BAC=22.5°，
∵点E与点D关于AB对称，
∴△AEB≌△ADB，
∴AE=AD，∠AEB=∠ADB=90°，∠EAB=∠DAB，
∴∠EAD=2∠DAB=45°，
同理：AF=AD，∠AFC=90°，∠DAF=45°，
∴AE=AF，∠EAF=∠EAD+∠DAF=90°，
∴四边形AEGF是正方形；
（2）四边形AEGF是正方形，
由（1）可知：∠EAB+∠FAC=∠BAC=45°，
∴∠EAF=90°，
∵∠AEB=∠AFC=90°，AE=AF，
∴四边形AEGF是正方形；
（3）设AD=x，则AE=EG=GF=x，
∴BG=x-2，CG=x-3，
∴（x-2）²+（x-3）²=5²，
解得x₁=6，x₂=-1（舍）
∴AD=x=6。