Question

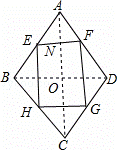
依次连接菱形各边中点所得到的四边形是　

Answer 1

矩形　．

考点：	矩形的判定；平行线的性质；三角形中位线定理；平行四边形的判定；菱形的性质．
专题：	证明题．
分析：	连接AC、BD交于O，根据三角形的中位线定理推出EF∥BD∥HG，EH∥AC∥FG，得出四边形EFGH是平行四边形，根据菱形性质推出AC⊥BD，推出EF⊥EH，即可得出答案．
解答：	解： 连接AC、BD交于O， ∵E、F、G、H分别是AB、AD、CD、BC的中点， ∴EF∥BD，FG∥AC，HG∥BD，EH∥AC， ∴EF∥HG，EH∥FG， ∴四边形EFGH是平行四边形， ∵四边形ABCD是菱形， ∴AC⊥BD， ∵EF∥BD，EH∥AC， ∴EF⊥EH， ∴∠FEH=90°， ∴平行四边形EFGH是矩形， 故答案为：矩形．
点评：	本题考查了矩形的判定，菱形的性质，平行四边形的判定，平行线性质等知识点的运用，主要考查学生能否正确运用性质进行推理，题目比较典型，难度适中．