题目内容
观察下面一列数，探索规律：-
，
，-
，
，-
，
，…写出第100个数是
，第2009个数是
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
| 5 |
| 6 |
| 6 |
| 7 |
| 100 |
| 101 |
| 100 |
| 101 |
-
| 2009 |
| 2010 |
-
；这一列数无限排列下去，与| 2009 |
| 2010 |
-1
-1
、1
1
两个数越来越接近．分析：观察不难发现，分子是从1开始的连续自然数，分母比分子大1，并且第奇数个数是负数，第偶数个数是正数，然后解答即可．
解答：解：∵-
，
，-
，
，-
，
，…，
∴第100个数是
，
第2009个数是-
；
这一列数无限排列下去，与-1、1两个数越来越接近．
故答案为：
；-
；-1、1．
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
| 5 |
| 6 |
| 6 |
| 7 |
∴第100个数是
| 100 |
| 101 |
第2009个数是-
| 2009 |
| 2010 |
这一列数无限排列下去，与-1、1两个数越来越接近．
故答案为：
| 100 |
| 101 |
| 2009 |
| 2010 |
点评：本题是对数字变化规律的考查，从分子与分母的关系，以及正负情况两个方面考虑求解是解题的关键，也是本题的难点．
练习册系列答案
活力课时同步练习册系列答案
相关题目
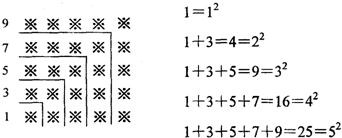
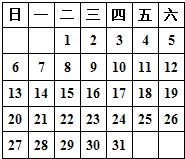
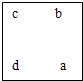
组成的图案和算式，解答问题：
