��Ŀ����
�ס�����У�μ�ij�н����־ٰ�ij�����Ӣ����ᄎ������У����������ȣ�������������ѧ���ɼ��ֱ�Ϊ7�֡�8�֡�9�֡�l0�֣�����Ϊ10�֣�������ͳ�����ݻ����������в�������ͳ��ͼ����
��У�ɼ�ͳ�Ʊ�
��1����ͼ1�У���7�֡��������ε�Բ�Ľǵ��� ��
��2�����㽫ͼ2������ͳ��ͼ����������
��3�������㣬��У��ƽ������8.3�֣���λ����8�֣��������У��ƽ���֡���λ����
��4�����Ҫ��ͬһ��ѧУѡȡ8�˵Ĵ����Ӳμ��м����������н����־�����������ѧУ�е�һ����ѡ����ѡ�֣�Ӧѡ����ѧУ��

��У�ɼ�ͳ�Ʊ�
| ���� | 7�� | 8�� | 9�� | 10�� |
| ���� | 11 | 0 | ���� | 8 |
��2�����㽫ͼ2������ͳ��ͼ����������
��3�������㣬��У��ƽ������8.3�֣���λ����8�֣��������У��ƽ���֡���λ����
��4�����Ҫ��ͬһ��ѧУѡȡ8�˵Ĵ����Ӳμ��м����������н����־�����������ѧУ�е�һ����ѡ����ѡ�֣�Ӧѡ����ѧУ��

���㣺����ͳ��ͼ,����ͳ��ͼ,��Ȩƽ����,��λ��
ר�⣺
��������1������360���ȥ���������Ӧ��Բ�ĽǼ�����⣻
��2�����������У������������������óɼ���8�ֵ��������Ӷ�������ͳ��ͼ����������
��3��������õ÷���9�ֵ�������Ȼ�����ƽ������ʽ����λ���Ķ�����⣻
��4��ֻҪ�Ƚ�ÿ��ѧУǰ8���ijɼ����ɣ�
��2�����������У������������������óɼ���8�ֵ��������Ӷ�������ͳ��ͼ����������
��3��������õ÷���9�ֵ�������Ȼ�����ƽ������ʽ����λ���Ķ�����⣻
��4��ֻҪ�Ƚ�ÿ��ѧУǰ8���ijɼ����ɣ�
����⣺��1����7�֡��������ε�Բ�Ľǵ���360��-90��-72��-54��=144�㣻
��2����У�������������ǣ�4��
=20���ˣ���
��ɼ���8�ֵ������ǣ�20-8-4-5=3���ˣ���
 ��
��
��3����У�е÷���9�ֵ������ǣ�20-11-8=1���ˣ���
���У��ƽ�����ǣ�
=8.3���֣���
��У����λ���ǣ�7�֣�
��4���÷���10�ֵ�������8�ˣ����Ұ�÷���10�ֵ���5�ˣ�����8�ˣ���Ӧѡ���У��
��2����У�������������ǣ�4��
| 72 |
| 360 |
��ɼ���8�ֵ������ǣ�20-8-4-5=3���ˣ���
 ��
����3����У�е÷���9�ֵ������ǣ�20-11-8=1���ˣ���
���У��ƽ�����ǣ�
| 7��11+8��0+9��1+10��8 |
| 20 |
��У����λ���ǣ�7�֣�
��4���÷���10�ֵ�������8�ˣ����Ұ�÷���10�ֵ���5�ˣ�����8�ˣ���Ӧѡ���У��
���������⿼���������ͳ��ͼ������ͳ��ͼ���ۺ����ã�����ͳ��ͼ���Ӳ�ͬ��ͳ��ͼ�еõ���Ҫ����Ϣ�ǽ������Ĺؼ�������ͳ��ͼ������ر�ʾ��ÿ����Ŀ�����ݣ�����ͳ��ͼֱ�ӷ�ӳ����ռ����İٷֱȴ�С��

��ϰ��ϵ�д�
�����Ŀ
���a��b=-a��a��0������ôb���ڣ�������
| A��1 | B��-1 | C��0 | D����1 |
����������ȷ���ǣ�������
| A��3a+2b=5ab |
| B��3a2b-3ba2=0 |
| C��3x2+2x3=5x5 |
| D��3y2-2y2=1 |
 ��ͼ��ֱ��Ϊһ�κ���y=kx+b��ͼ����y��0ʱ����x
��ͼ��ֱ��Ϊһ�κ���y=kx+b��ͼ����y��0ʱ����x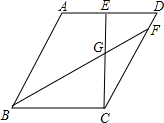 ��ͼ����?ABCD�У�CE��AD�ڵ�E����CB=CE����FΪCD���ϵ�һ�㣬CB=CF������BF��CE�ڵ�G��
��ͼ����?ABCD�У�CE��AD�ڵ�E����CB=CE����FΪCD���ϵ�һ�㣬CB=CF������BF��CE�ڵ�G��