题目内容
已知一扇形的圆心角是120°,它所对的弧长是12π,则扇形面积为
108π
108π
;用该扇形围成一个圆锥,则该圆锥的底面半径是6
6
.分析:根据扇形弧长公式求得该扇形的半径,然后根据扇形面积公式求解;设圆锥底面的半径为r,由于圆锥的侧面展开图为扇形,扇形的弧长等于圆锥底面圆的周长.
解答:解:设该扇形的半径为R.则
=12π,
解得R=18.
所以,该扇形的面积=
=108π;
设圆锥底面的半径为r,
根据题意得2πr=12π,
解得r=6.
故答案分别是:108π;6.
| 120π×R |
| 180 |
解得R=18.
所以,该扇形的面积=
| 120π×182 |
| 360 |
设圆锥底面的半径为r,
根据题意得2πr=12π,
解得r=6.
故答案分别是:108π;6.
点评:本题考查了扇形面积的计算和圆锥的计算:圆锥的侧面展开图为扇形,扇形的弧长等于圆锥底面圆的周长.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 er Life)”为主题的世博知识竞赛,竞赛规定得分最多的班级为优胜班级.各代表队比赛结果如下:
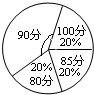
er Life)”为主题的世博知识竞赛,竞赛规定得分最多的班级为优胜班级.各代表队比赛结果如下: 如图是某校九年级(1)班一次课外活动情况的扇形统计图.已知九年级(1)班共有54人.据统计,这次课外活动中,参加读书活动的有18人,参加科技活动占全班总人数的
如图是某校九年级(1)班一次课外活动情况的扇形统计图.已知九年级(1)班共有54人.据统计,这次课外活动中,参加读书活动的有18人,参加科技活动占全班总人数的