题目内容
已知矩形ABCD的周长是24 cm，点M是CD中点，∠AMB=90°，则AB=________cm，AD=________cm．
8 4
分析：本题应用矩形的性质，求解即可．
解答：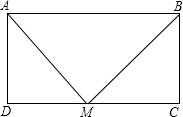
解：∵ABCD为矩形
∴AD=BC，∠D=∠C=90°
∵点M是CD中点
∴DM=CM
∴△ADM≌△BCM
∴AM=BM
∵∠AMB=90°
∴△AMB为等腰直角三角形
∴AD=DM=
DC
∵矩形ABCD的周长是24 cm
∴2（AD+DC）=6AD=24cm
∴AD=4cm，AB=8cm．
故答案为8，4．
点评：此题主要考查学生对矩形的性质的运用．
分析：本题应用矩形的性质，求解即可．
解答：
解：∵ABCD为矩形∴AD=BC，∠D=∠C=90°
∵点M是CD中点
∴DM=CM
∴△ADM≌△BCM
∴AM=BM
∵∠AMB=90°
∴△AMB为等腰直角三角形
∴AD=DM=
DC∵矩形ABCD的周长是24 cm
∴2（AD+DC）=6AD=24cm
∴AD=4cm，AB=8cm．
故答案为8，4．
点评：此题主要考查学生对矩形的性质的运用．
练习册系列答案
相关题目
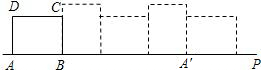地转动，当它转动一周时（A→A′），顶点A所经过的路线长等于