Question

【题目】如图1，在平面直角坐标系xOy中，抛物线y=ax2+1经过点A（4，﹣3），顶点为点B，点P为抛物线上的一个动点，l是过点（0，2）且垂直于y轴的直线，过P作PH⊥l，垂足为H，连接PO．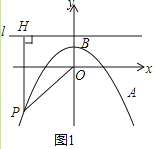
（1）求抛物线的解析式，并写出其顶点B的坐标；
（2）①当P点运动到A点处时，计算：PO= ， PH= ， 由此发现，POPH（填“＞”、“＜”或“=”）；
②当P点在抛物线上运动时，猜想PO与PH有什么数量关系，并证明你的猜想；
（3）如图2，设点C（1，﹣2），问是否存在点P，使得以P，O，H为顶点的三角形与△ABC相似？若存在，求出P点的坐标；若不存在，请说明理由．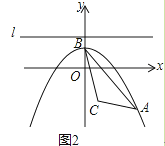

Answer 1

【答案】
（1）

解：∵抛物线y=ax2+1经过点A（4，﹣3），

∴﹣3=16a+1，

∴a=﹣ ，

∴抛物线解析式为y=﹣ x2+1，顶点B（0，1）．

（2）①5；5；=；②结论：PO=PH．
理由：设点P坐标（m，﹣ m2+1），
∵PH=2﹣（﹣ m2+1）= m2+1
PO= = m2+1，
∴PO=PH
（3）

解：∵BC= = ，AC= = ，AB= =4

∴BC=AC，

∵PO=PH，

又∵以P，O，H为顶点的三角形与△ABC相似，

∴PH与BC，PO与AC是对应边，

∴ ，设点P（m，﹣ m2+1），

∴ ，

解得m=±1，

∴点P坐标（1， ）或（﹣1， ）．

【解析】（2）①当P点运动到A点处时，∵PO=5，PH=5，
∴PO=PH，
故答案分别为5，5，=．
【考点精析】本题主要考查了二次函数的性质的相关知识点，需要掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．