题目内容
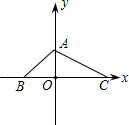已知，如图，在平面直角坐标系中，S△ABC=24，OA=OB，BC=12，求△ABC三个顶点的坐标．
解：∵S△ABC=
BC•OA=24，OA=OB，BC=12，
∴OA=OB=
=
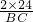=4，
∴OC=8，
∵点O为原点，
∴A（0，4），B（-4，0），C（8，0）．
分析：首先根据面积求得OA的长，再根据已知条件求得OB的长，最后求得OC的长．最后写坐标的时候注意点的位置．
点评：写点的坐标的时候，特别注意根据点所在的位置来确定坐标符号．
BC•OA=24，OA=OB，BC=12，∴OA=OB=
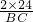==4，∴OC=8，
∵点O为原点，
∴A（0，4），B（-4，0），C（8，0）．
分析：首先根据面积求得OA的长，再根据已知条件求得OB的长，最后求得OC的长．最后写坐标的时候注意点的位置．
点评：写点的坐标的时候，特别注意根据点所在的位置来确定坐标符号．
练习册系列答案
相关题目
如图，在平面直角坐标系中，直
如图，在平面直角坐标系中，原点O处有一乒乓球发射器向空中发射乒乓球，乒乓球飞行路线是一条抛物线，在地面上落点落在X轴上为点B．有人在线段OB上点C（靠点B一侧）竖直向上摆放无盖的圆柱形桶，试图让乒乓球落入桶内．已知OB=4米，OC=3米，乒乓球飞行最大高度MN=5米，圆柱形桶的直径为0.5，高为0.3米（乒乓球的体积和圆柱形桶的厚度忽略不计）．
