题目内容
用总长为32m的篱笆墙围成一个扇形的花园.
(1)当扇形花园的半径为6m时,求扇形花园的面积;
(2)设扇形花园的半径为x(m),面积为y(m2),求y关于x的函数关系式,并写出x的取值范围;
(3)当扇形花园的半径为多少时,花园的面积最大?最大面积是多少?此时,这个扇形的圆心角约是多少度?(精确到0.1度)
解:(1)∵扇形花园的半径为6m,
∴扇形的弧长=32-2×6=20,
∴扇形花园的面积= ×6×20=60(cm2);
×6×20=60(cm2);
(2)∵扇形花园的半径为x,
∴扇形的弧长=32-2x,
∴y= •x•(32-2x)
•x•(32-2x)
=-x2+16x (0<x<16);
(3)y=-x2+16x
=-(x-8)2+64,
∵a=-1<0,
∴当x=8时,y取最大值64;
∴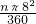 =64,解得n=114.6度.
=64,解得n=114.6度.
所以这个扇形的圆心角=约为114.6度.
分析:(1)先计算出弧长为20cm,然后根据扇形的面积根据计算即可;
(2)先得到扇形的弧长=32-2x,然后根据扇形的面积得到y= •x•(32-2x),整理即可;
•x•(32-2x),整理即可;
(3)把y=-x2+16x 配成顶点式y=-(x-8)2+64,然后根据二次函数的最值问题进行回答即可,最后根据扇形的面积公式计算此时扇形的圆心角.
点评:本题考查了二次函数的应用:先得到二次函数的顶点式y=a(x-h)2+k,当a<0,x=h时,y有最大值k;当a<0,x=h时,y有最小值k.也考查了扇形的面积公式.
∴扇形的弧长=32-2×6=20,
∴扇形花园的面积=
 ×6×20=60(cm2);
×6×20=60(cm2);(2)∵扇形花园的半径为x,
∴扇形的弧长=32-2x,
∴y=
 •x•(32-2x)
•x•(32-2x)=-x2+16x (0<x<16);
(3)y=-x2+16x
=-(x-8)2+64,
∵a=-1<0,
∴当x=8时,y取最大值64;
∴
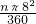 =64,解得n=114.6度.
=64,解得n=114.6度.所以这个扇形的圆心角=约为114.6度.
分析:(1)先计算出弧长为20cm,然后根据扇形的面积根据计算即可;
(2)先得到扇形的弧长=32-2x,然后根据扇形的面积得到y=
 •x•(32-2x),整理即可;
•x•(32-2x),整理即可;(3)把y=-x2+16x 配成顶点式y=-(x-8)2+64,然后根据二次函数的最值问题进行回答即可,最后根据扇形的面积公式计算此时扇形的圆心角.
点评:本题考查了二次函数的应用:先得到二次函数的顶点式y=a(x-h)2+k,当a<0,x=h时,y有最大值k;当a<0,x=h时,y有最小值k.也考查了扇形的面积公式.

练习册系列答案
相关题目