题目内容
已知在△ABC中,AB=AC,sinB= ,且△ABC的周长为36,则此三角形的面积为
,且△ABC的周长为36,则此三角形的面积为
- A.12
- B.24
- C.48
- D.96
C
分析:设AD=3a,则AB=5a=AC,由勾股定理求出BD=4a,根据等腰三角形的性质得出BD=DC=4a,根据已知得出5a+5a+4a+4a=36,求出a,求出BC和AD,根据三角形的面积公式求出即可.
解答:
过A作AD⊥BC于D,
∵sinB= =
= ,
,
∴设AD=3a,则AB=5a=AC,由勾股定理得:BD=4a,
∵AB=AC,AD⊥BC,
∴BD=DC=4a,
∵△ABC的周长为36,
∴5a+5a+4a+4a=36,
a=2,
∴BC=4a+4a=16,AD=3a=6,
∴△ABC的面积是 BC×AD=
BC×AD= ×16×6=48,
×16×6=48,
故选C.
点评:本题考查了解直角三角形、三角形的面积、勾股定理、等腰三角形的性质等知识点,关键是得出关于a的方程和构造直角三角形,题目具有一定的代表性,是一道比较好的题目.
分析:设AD=3a,则AB=5a=AC,由勾股定理求出BD=4a,根据等腰三角形的性质得出BD=DC=4a,根据已知得出5a+5a+4a+4a=36,求出a,求出BC和AD,根据三角形的面积公式求出即可.
解答:

过A作AD⊥BC于D,
∵sinB=
 =
= ,
,∴设AD=3a,则AB=5a=AC,由勾股定理得:BD=4a,
∵AB=AC,AD⊥BC,
∴BD=DC=4a,
∵△ABC的周长为36,
∴5a+5a+4a+4a=36,
a=2,
∴BC=4a+4a=16,AD=3a=6,
∴△ABC的面积是
 BC×AD=
BC×AD= ×16×6=48,
×16×6=48,故选C.
点评:本题考查了解直角三角形、三角形的面积、勾股定理、等腰三角形的性质等知识点,关键是得出关于a的方程和构造直角三角形,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.
22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.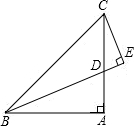 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC.
如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC. 如图,已知在△ABC中,∠B与∠C的平分线交于点P.
如图,已知在△ABC中,∠B与∠C的平分线交于点P.