题目内容
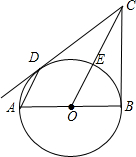
如图四边形ABCD内接于⊙O，AB为直径，PD切⊙O于D，与BA延长线交于P点，已知∠BCD=130°，则∠ADP=______．
连接BD，
∵四边形ABCD内接于⊙O，∠BCD=130°，
∴∠BAD=50°，
∵AB为直径，
∴∠ADB=90°，
∴∠ABD=∠40°
∵PD切⊙O于D，
∴∠ADP=∠ABD=40°，
故答案为：40°．
∵四边形ABCD内接于⊙O，∠BCD=130°，
∴∠BAD=50°，
∵AB为直径，
∴∠ADB=90°，
∴∠ABD=∠40°
∵PD切⊙O于D，
∴∠ADP=∠ABD=40°，
故答案为：40°．
练习册系列答案
相关题目
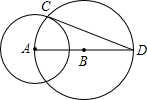
延长线分别交AC、BC于点G、F．
