Question

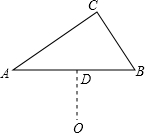已知，如图△ABC为直角三角形，且∠C=90°，点D是AB的中点，OD⊥AB，并且OD=

1

2

AB．
（1）试画出将△ABC绕点O按顺时针方向连续旋转三次，每次旋转90°的图形；
（2）你能利用作好的图形证明勾股定理吗？

Answer 1

分析：（1）利用旋转的性质，找出各个关键点的对应点，连接即可．
（2）设Rt△ABC中，AC=b，BC=a，AB=c，则可证四边形CFED为正方形、又可证四边形AMNB为一边长为c的小正方形．故(a+b)2=4×

1

2

ab+c2、化简得a²+b²=c²．

解答：解：（1）连续旋转三次每次旋转90°所得图形如下图所示；

（2）如图，设Rt△ABC中，AC=b，BC=a，AB=c，
∵△ABC绕点O按顺时针方向连续旋转三次，每次旋转90°，OD=

1

2

AB，
∴四边形CFED为正方形，四边形AMNB为一边长为c的小正方形，
由正方形面积相等可得：
(a+b)2=4×

1

2

ab+c2，
化简得a²+b²=c²．

点评：本题考查了旋转图形的画法以及勾股定理的证明．