题目内容
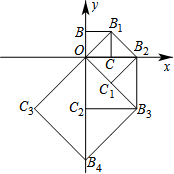 如图,点O(0,0),B(0,1)是正方形OBB1C的两个顶点,以它的对角线OB1为一边作正方形OB1B2C1,以正方形OB1B2C1的对角线OB2为一边作正方形OB2B3C2,写出点B3的坐标为
如图,点O(0,0),B(0,1)是正方形OBB1C的两个顶点,以它的对角线OB1为一边作正方形OB1B2C1,以正方形OB1B2C1的对角线OB2为一边作正方形OB2B3C2,写出点B3的坐标为(2,-2)
(2,-2)
;再以正方形OB2B3C2的对角线OB3为一边作正方形OB3B4C3,…依此规律作下去,点B2013的坐标为(-21006,-21006)
(-21006,-21006)
.分析:根据题意和图形可看出每经过一次变化,都顺时针旋转45°,边长都乘以
,所以可求出从B到B3的后变化的坐标,再求出B1、B2、B3、B4、B5、B6、B7、B8、B9的坐标,找出这些坐标的之间的规律,然后根据规律计算出点B2013的坐标.
| 2 |
解答:解:根据题意和图形可看出每经过一次变化,都顺时针旋转45°,边长都乘以
,
∵从B到B3经过了3次变化,
∵45°×3=135°,1×(
)3=2
.
∴点B3所在的正方形的边长为2
,点B3位置在第四象限.
∴点B3的坐标是(2,-2);
可得出:B1点坐标为(1,1),
B2点坐标为(0,2),
B3点坐标为(2,-2),
B4点坐标为(0,-4),B5点坐标为(-4,-4),
B6(-8,0),B7(-8,8)
B8(0,16),B9(16,16),
由规律可以发现,每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变为原来的
倍,
∵2013÷8=251…5,
∴B2013的纵横坐标符号与点B5的相同,纵横坐标都是负值,
∴B2013的坐标为(-21006,-21006).
故答案为:(2,-2),(-21006,-21006).
| 2 |
∵从B到B3经过了3次变化,
∵45°×3=135°,1×(
| 2 |
| 2 |
∴点B3所在的正方形的边长为2
| 2 |
∴点B3的坐标是(2,-2);
可得出:B1点坐标为(1,1),
B2点坐标为(0,2),
B3点坐标为(2,-2),
B4点坐标为(0,-4),B5点坐标为(-4,-4),
B6(-8,0),B7(-8,8)
B8(0,16),B9(16,16),
由规律可以发现,每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变为原来的
| 2 |
∵2013÷8=251…5,
∴B2013的纵横坐标符号与点B5的相同,纵横坐标都是负值,
∴B2013的坐标为(-21006,-21006).
故答案为:(2,-2),(-21006,-21006).
点评:本题主要考查正方形的性质和坐标与图形的性质的知识点,解答本题的关键是由点坐标的规律发现每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变为原来的
倍,此题难度较大.
| 2 |

练习册系列答案
相关题目
 如图,点A的坐标为(2
如图,点A的坐标为(2| 2 |
| A、(0,0) | ||||||||
B、(
| ||||||||
| C、(1,1) | ||||||||
D、(
|

 BE、CD、CE,已知∠BED=30°.
BE、CD、CE,已知∠BED=30°.
 12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是
12、如图,点O到直线l的距离为3,如果以点O为圆心的圆上只有两点到直线l的距离为1,则该圆的半径r的取值范围是