题目内容
如图，OA⊥OB，∠BOC=30°，OD平分∠AOC，则∠BOD=
- A.60°
- B.50°
- C.40°
- D.30°
D
试题分析：由OA⊥OB，∠BOC=30°可得∠AOC的度数，再根据角平分线的性质可得∠AOD的度数，从而求得结果.
∵OA⊥OB，∠BOC=30°
∴∠AOC=120°
∵OD平分∠AOC
∴∠AOD=60°
∴∠BOD=30°
故选D.
考点：比较角的大小，角平分线的性质
点评：解题的关键是熟练掌握角的平分线把角分成相等的两个小角，且都等于大角的一半.
试题分析：由OA⊥OB，∠BOC=30°可得∠AOC的度数，再根据角平分线的性质可得∠AOD的度数，从而求得结果.
∵OA⊥OB，∠BOC=30°
∴∠AOC=120°
∵OD平分∠AOC
∴∠AOD=60°
∴∠BOD=30°
故选D.
考点：比较角的大小，角平分线的性质
点评：解题的关键是熟练掌握角的平分线把角分成相等的两个小角，且都等于大角的一半.
练习册系列答案
英才计划同步课时高效训练系列答案
相关题目
（2013•玉田县一模）如图，OA⊥OB，△CDE的边CD在OB上，∠ECD=45°．将△CDE绕点C逆时针旋转75°，点E的对应点N恰好落在OA上，则
如图，OA=OB，OC=OD，∠O=50°，∠D=30°，则∠AEC等于（ ）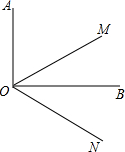
如图，OA⊥OB，OB平分∠MON，若∠AON=120°，求∠AOM的度数．
如图，OA⊥OB，∠COD为平角，若OC平分∠AOB，则∠BOD=