题目内容
 如图,三角形ABC各边的四等分点D,E,F分别与点C,B,A相连,得到一个小三角形GHI,那么三角形GHI的面积与三角形ABC的面积的比是________.
如图,三角形ABC各边的四等分点D,E,F分别与点C,B,A相连,得到一个小三角形GHI,那么三角形GHI的面积与三角形ABC的面积的比是________.
11:16
分析:可作AG∥BC交BE延长线于点G,作DH∥AB交CF于点H,由平行线分线段成比例可得线段之间的比例关系,进而转化为三角形的面积关系,即可求解结论.
解答: 解:作AP∥BC交BE延长线于点P,作DQ∥AB交CF于点H,则得:
解:作AP∥BC交BE延长线于点P,作DQ∥AB交CF于点H,则得:
AP:BC=AE:EC=1:3,AP:BD=1:1,
又∵DQ:BF=1:4,DQ:AF=1:12,
∴DI:AI=1:12,DI:DA=1:13,
从而S△CDI= S△BFC=
S△BFC= S△ABC,
S△ABC,
∴S△GHI:S△ABC=11:16.
故答案是:11:16.
点评:本题主要考查了平行线分线段成比例的性质以及三角形的性质和面积问题,能够熟练运用平行线的性质求解一些计算问题,难度较大.
分析:可作AG∥BC交BE延长线于点G,作DH∥AB交CF于点H,由平行线分线段成比例可得线段之间的比例关系,进而转化为三角形的面积关系,即可求解结论.
解答:
 解:作AP∥BC交BE延长线于点P,作DQ∥AB交CF于点H,则得:
解:作AP∥BC交BE延长线于点P,作DQ∥AB交CF于点H,则得:AP:BC=AE:EC=1:3,AP:BD=1:1,
又∵DQ:BF=1:4,DQ:AF=1:12,
∴DI:AI=1:12,DI:DA=1:13,
从而S△CDI=
 S△BFC=
S△BFC= S△ABC,
S△ABC,∴S△GHI:S△ABC=11:16.
故答案是:11:16.
点评:本题主要考查了平行线分线段成比例的性质以及三角形的性质和面积问题,能够熟练运用平行线的性质求解一些计算问题,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
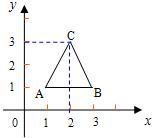 20、如图,三角形ABC的顶点分别为A(1,1)、B(3,1)、C(2,3).
20、如图,三角形ABC的顶点分别为A(1,1)、B(3,1)、C(2,3).

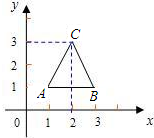 如图,三角形ABC的顶点分别为A(1,1)、B(3,1)、C(2,3).
如图,三角形ABC的顶点分别为A(1,1)、B(3,1)、C(2,3).