题目内容
已知关于x的一元二次方程
有两个不相等的实数根，求k的取值范围．
解：由题意得：1-2k≠0即k≠
，
k+1≥0，即k≥-1
△=b2-4ac=（-2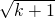
）2-4×（1-2k）×（-1）=8-4k＞0，
∴k＜2
综合所述，得-1≤k＜2且
，
分析：一元二次方程有两个不相等的实数根，则△=b2-4ac＞0，结合一元二次方程的定义，求出k的取值范围．
点评：1、一元二次方程根的情况与判别式△的关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根
2、切记不要忽略一元二次方程二次项系数不为零这一隐含条件．
，k+1≥0，即k≥-1
△=b2-4ac=（-2
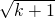）2-4×（1-2k）×（-1）=8-4k＞0，∴k＜2
综合所述，得-1≤k＜2且
，分析：一元二次方程有两个不相等的实数根，则△=b2-4ac＞0，结合一元二次方程的定义，求出k的取值范围．
点评：1、一元二次方程根的情况与判别式△的关系：
（1）△＞0?方程有两个不相等的实数根；
（2）△=0?方程有两个相等的实数根；
（3）△＜0?方程没有实数根
2、切记不要忽略一元二次方程二次项系数不为零这一隐含条件．
练习册系列答案
相关题目
已知关于x的一元二次x2-6x+k+1=0的两个实数根x1，x2，
+
=1，则k的值是（ ）
| 1 |
| x1 |
| 1 |
| x2 |
| A、8 | B、-7 | C、6 | D、5 |
．
．