题目内容
在同一直角坐标系中，画出一次函数y=-x+2与y=2x+2的图象，并求出这两条直线与x轴围成的三角形的面积与周长．分析：作出两个函数的图象，求出图象与坐标轴的交点以及两个函数图象的交点．进而可求出三角形的面积与周长．
解答：
解：如图：直线y=-x+2与x轴的交点为B（-1，0），
直线y=2x+2与x轴的交点为C（2，0）；
两个函数的交点是A（0，2）；
∴BC=3，AB=
=
，AC=2
；
则S△ABC=
BC•OA=3；C△ABC=
+2
+3．
解：如图：直线y=-x+2与x轴的交点为B（-1，0），直线y=2x+2与x轴的交点为C（2，0）；
两个函数的交点是A（0，2）；
∴BC=3，AB=
| OB2+OA2 |
| 5 |
| 2 |
则S△ABC=
| 1 |
| 2 |
| 5 |
| 2 |
点评：本题考查了一次函数与二元一次方程组的关系，三角形的面积与周长．
练习册系列答案
相关题目
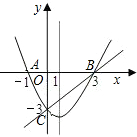如图，在同一直角坐标系中，二次函数的图象与两坐标轴分别交于A（-1，0）、点B（3，0）和点C（0，-3），一次函数的图象与抛物线交于B、C两点．
爱动脑筋的小明同学在买一双新的运动鞋时，发现了一些有趣现象，即鞋子的号码与鞋子的长（cm）之间存在着某种联系，经过收集数据，得到下表：