题目内容
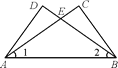
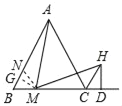
【题目】已知,M是等边△ABC边BC上的点,如图,连接AM,过点M作∠AMH=60°,MH与∠ACB的邻补角的平分线交于点H,过H作HD⊥BC于点D
(1)求证:MA=MH
(2)猜想写出CB、CM、CD之间的数量关系式,并加以证明.

【答案】(1)见解析;(2)CB=CM+2CD.
【解析】(1)过M点作MN∥AC交AB于N,然后根据全等三角形的判定“ASA”证明△AMN≌△MHC,再根据全等三角形的性质可得MA=MH;
(2)过M点作MG⊥AB于G,再根据全等三角形的判定“AAS”证明△BMG≌△CHD可得CD=BG,因为BM=2CD可得BC=MC+2CD.
(1)如图,过M点作MN∥AC交AB于N,
则BM=BN,∠ANM=120°,
∵AB=BC,
∴AN=MC,
∵CH是∠ACD的平分线,
∴∠ACH=60°=∠HCD,
∴∠MCH=∠ACB+∠ACH=120°,
又∵∠NMC=120°,∠AMH=60°,
∴∠HMC+∠AMN=60°
又∵∠NAM+∠AMN=∠BNM=60°,
∴∠HMC=∠MAN,
在△ANM和△MCH中,
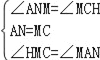 ,
,
∴△AMN≌△MHC(ASA),
∴MA=MH;
(2)CB=CM+2CD;
证明:如图,过M作MG⊥AB于G,
∵HD⊥BC,
∴∠HDC=∠MGB=90°,
∵△AMN≌△MHC,
∴MN=HC,
∵MN=MB,
∴HC=BM,
在△BMG和△CHD中,
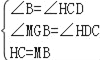 ,
,
∴△BMG≌△CHD(AAS),
∴CD=BG,
∵△BMN为等边三角形,
∴BM=2BG,
∴BM=2CD,
∴BC=MC+2CD.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目