题目内容
已知正方形ABCD,过C的直线分别交AD,AB的延长线于点E,F,且AE=15,AF=10,求正方形ABCD的边长.分析:根据题意,易证△FBC∽△FAE,利用三角形相似比
=
,列方程求解即可.
| BC |
| AE |
| FB |
| FA |
解答: 解:∵BC∥AE
解:∵BC∥AE
∴△FBC∽△FAE
∴
=
设正方形边长为x
则
=
∴x=6.
即正方形边长为6.
 解:∵BC∥AE
解:∵BC∥AE∴△FBC∽△FAE
∴
| BC |
| AE |
| FB |
| FA |
设正方形边长为x
则
| x |
| 15 |
| 10-x |
| 10 |
∴x=6.
即正方形边长为6.
点评:主要考查了正方形的性质和相似三角形的判定;充分利用正方形的特殊性质来找到相似的条件,从而判定全等后利用相似三角形的性质解题.注意:常用相似中的比例线段作为相等关系列方程.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
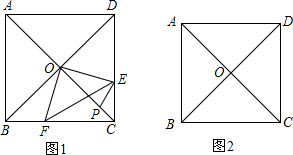
 直至点G与点B重合为止.设x秒时Rt△EFG与正方形ABCD重叠部分的面积记为ycm2.
直至点G与点B重合为止.设x秒时Rt△EFG与正方形ABCD重叠部分的面积记为ycm2. 已知正方形ABCD的边长为4厘米,E,F分别为边DC,BC上的点,BF=1厘米,CE=2厘米,BE,DF相交于点G,求四边形CEGF的面积.
已知正方形ABCD的边长为4厘米,E,F分别为边DC,BC上的点,BF=1厘米,CE=2厘米,BE,DF相交于点G,求四边形CEGF的面积.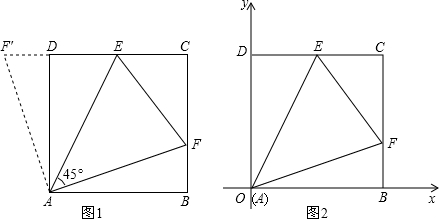
 如图,已知正方形ABCD边长为2,E、F、G、H分别为各边上的点,且AE=BF=CG=DH.
如图,已知正方形ABCD边长为2,E、F、G、H分别为各边上的点,且AE=BF=CG=DH.